Question
Question: A fish is at a depth of 12cm. It \(\left( {\mu = \dfrac{4}{3}} \right)\) is viewed by an observer on...
A fish is at a depth of 12cm. It (μ=34) is viewed by an observer on the bank of the lake. Its apparent depth, as observed by the observer, is
A. 3cm
B. 9cm
C. 12cm
D. 16cm
Solution
To calculate the distance measured by the object measured by an observer from point C. We will use the formula:
Refractive index, μ=apparent depth (h)real depth (H)
Where real depth is the distance object from the surface of a material medium while apparent depth is the distance of image formed due to the refraction from the material medium surface.
Complete step by step answer:
According to question, Real depth of fish = 12cm
And the refractive index of the medium μ=34
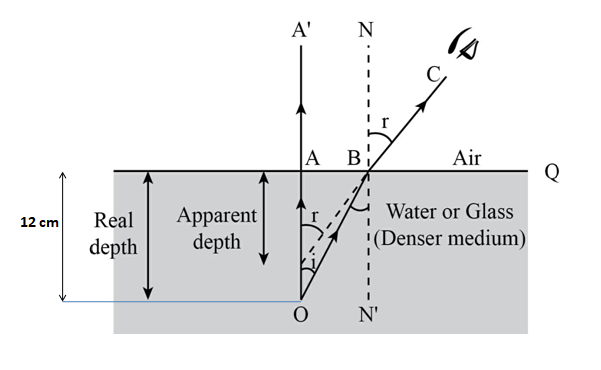
We know, μ=apparent depth (h)real depth (H)
∴34=apparent depth12
⇒apparent depth (h) = 43×12=9cm
Hence the apparent depth observed by the observer (h) =9cm. Therefore, the correct option is (B).
Additional information:
The apparent depth is always smaller than the real depth. If real depth increases, the apparent depth also increases. Thus, the graph of real depth d1 against the apparent depth d2 is a straight line graph passing through the origin. Therefore, the apparent depth is directly proportional to the real depth.
Note:
The depth of the image of an object submerged in a transparent medium; it is reduced from the real depth of the object by a factor equal to the relative index of refraction of the medium concerning air. Apparent depth varies with viewing angle. If the greater the viewing angle, the more the bending of the light, and therefore, the less the apparent depth formed.
