Question
Question: A fish is a little way below the surface of a lake. If the critical angle is \(49^{\circ}\), then th...
A fish is a little way below the surface of a lake. If the critical angle is 49∘, then the fish could see things above the water surface within an angular range at θ∘ where,
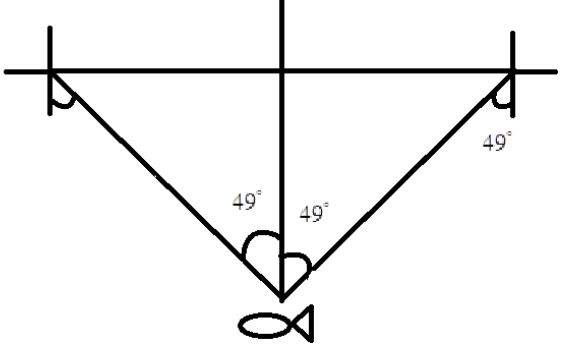
Solution
We know that the angle of inclination when the refracted ray just grazes the air-water surface is called the critical angle of incidence. Which says that, if the angle of incidence is equal to the critical angle then the refracted ray is equal to 90∘.
Formula used:
θ=2×i
Complete answer:
Here, we have an air-water combination and the fish is in the water.
We know that the vision of fish will cover a conical section as given in the figure. This is similar to when a candle is placed in a dark room; we can see that a conical area gets illuminated. This to say that the light rays from the candle, illuminates a conical section of the room.
Similarly, if instead of the candle, if we had an eye which is an optical device, it would be able to see the things which are inside this conical section. This conical section which is visible is called the peripheral vision of the eyes or the angular range of the eyes.
Given that the critical angle is 49∘.
Then we know that the angular range is twice the critical angle, then here angular range θ=2×49=98∘
This means that the fish will be able to see the things that will fall inside the 98∘of its vision.
Thus, D.θ=98∘ is the answer.
Note:
The critical angle for the air-water surface is 48.6∘. Which to say that any angle greater than the critical angle, suffers total internal reflection. Here, anyways the angle of refraction is not asked, but it is good to know the reason behind why the question says critical angle instead of just angle.
