Question

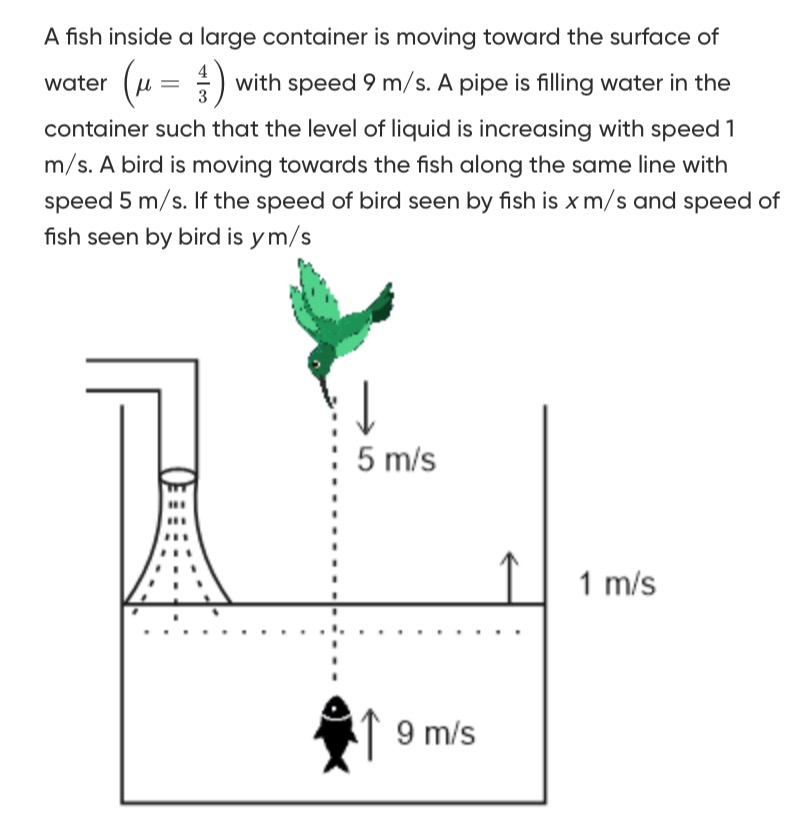
A fish inside a large container is moving toward the surface of water ($\mu = \frac{4}{3}$) with speed 9 m/s. A pipe is filling water in the container such that the level of liquid is increasing with speed 1 m/s. A bird is moving towards the fish along the same line with speed 5 m/s. If the speed of bird seen by fish is x m/s and speed of fish seen by bird is y m/s

Answer 1

x = 12.5 m/s, y = 50/3 m/s

Answer 2

To solve this problem, we need to consider the apparent velocities due to refraction and the relative motion of the objects and the water surface. We'll define upward direction as positive.

Given values: Refractive index of water, $\mu_w = \frac{4}{3}$ Refractive index of air, $\mu_a = 1$ Velocity of fish, $V_F = +9$ m/s (upwards) Velocity of water surface, $V_S = +1$ m/s (upwards) Velocity of bird, $V_B = -5$ m/s (downwards)

The general formula for the apparent velocity of an object (O) in medium 1 ($\mu_1$) as seen by an observer (I) in medium 2 ($\mu_2$), when the interface (S) is also moving, is: $V_{O,app/I} = \frac{\mu_1}{\mu_2} (V_O - V_S) + (V_S - V_I)$

1. Speed of bird seen by fish (x m/s): Here, the object is the bird (B) in air ($\mu_1 = \mu_a = 1$). The observer is the fish (F) in water ($\mu_2 = \mu_w = \frac{4}{3}$). $V_O = V_B = -5$ m/s $V_I = V_F = +9$ m/s $V_S = +1$ m/s

Using the formula: $x = V_{B,app/F} = \frac{\mu_a}{\mu_w} (V_B - V_S) + (V_S - V_F)$ $x = \frac{1}{4/3} (-5 - 1) + (1 - 9)$ $x = \frac{3}{4} (-6) + (-8)$ $x = -4.5 - 8$ $x = -12.5$ m/s

The speed of the bird seen by the fish is the magnitude of this velocity: $x = |-12.5|$ m/s = 12.5 m/s. The negative sign indicates that the bird appears to be moving downwards relative to the fish.

2. Speed of fish seen by bird (y m/s): Here, the object is the fish (F) in water ($\mu_1 = \mu_w = \frac{4}{3}$). The observer is the bird (B) in air ($\mu_2 = \mu_a = 1$). $V_O = V_F = +9$ m/s $V_I = V_B = -5$ m/s $V_S = +1$ m/s

Using the formula: $y = V_{F,app/B} = \frac{\mu_w}{\mu_a} (V_F - V_S) + (V_S - V_B)$ $y = \frac{4/3}{1} (9 - 1) + (1 - (-5))$ $y = \frac{4}{3} (8) + (1 + 5)$ $y = \frac{32}{3} + 6$ $y = \frac{32}{3} + \frac{18}{3}$ $y = \frac{50}{3}$ m/s

The speed of the fish seen by the bird is the magnitude of this velocity: $y = |\frac{50}{3}|$ m/s = $\frac{50}{3}$ m/s. The positive sign indicates that the fish appears to be moving upwards relative to the bird.