Question

A fish F, in the pond is at a depth of 0.8m from the water surface and is moving vertically upward with velocity 2ms-1. At the same instant, a bird B is at a height of 6m from the water surface and is moving downward with the velocity 3ms-1. At this instant, both are on the same vertical line as shown in the figure. Which of the following statements are correct?

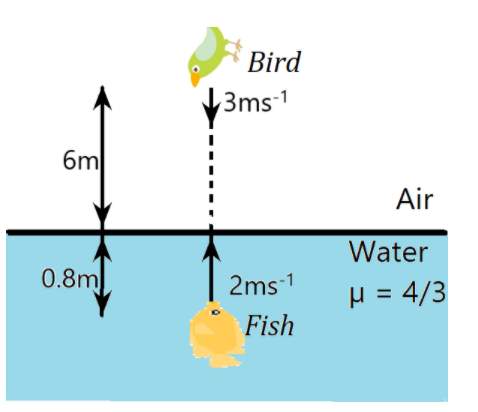
A. Height of B, observed by F from itself, is equal to 5.30m
B. Depth of F, observed by B from itself, is equal to 6.60m
C. Height of B, observed by F from itself, is equal to 8.80m
D. Depth of F, observed by B from itself, is equal to 4.50m

Answer 1

The question is clearly asking for actual depth and height at which the objects are viewed with respect to each other. They're the sum of apparent and real, depth and height respectively. Firstly, we need to find the apparent quantities and then add them to the actual quantities. The velocity does not affect the apparent depth or apparent height.
Formula used:
$\dfrac{{{d'}}}{{{\mu '}}} = \dfrac{d}{\mu }$
$\dfrac{h}{\mu } = \dfrac{{{h'}}}{{{\mu '}}}$

Complete answer:
It is given in the question, that the real depth of the F (fish) is 0.8m. The apparent depth of the fish is given by
$\dfrac{{{d'}}}{{{\mu '}}} = \dfrac{d}{\mu }$
Where
${d'}$ is the apparent depth of F
$d$ is the real depth
${\mu '}$ is the refractive index of air
$\mu$ is the refractive index of water
Substituting the values given in the question, we have
\eqalign{ & {\dfrac{d}{{{\mu '}}}'} = \dfrac{d}{\mu } \cr & \Rightarrow {d'} = \dfrac{{0.8}}{{\dfrac{4}{3}}} \times 1 = 0.6m \cr}
Thus, the depth of F, seen by B from itself, is equivalent to$0.6 + 6 = 6.6m$
Similarly, the apparent height can be found,
\eqalign{ & \dfrac{h}{\mu } = \dfrac{{{h'}}}{{{\mu '}}} \cr & \Rightarrow h = \mu \times \dfrac{{{h'}}}{{{\mu '}}} = \dfrac{4}{3} \times \dfrac{6}{1} = 8m \cr}
Here:
$h$ is the apparent height of B
${h'}$ is the real height
${\mu '}$ is the refractive index of air
$\mu$ is the refractive index of water
Thus, the height of B, seen by F from itself, is equivalent to $8 + 0.8 = 8.8m$

Therefore, the correct options are B and C.

Note:
If you find the apparent height and apparent depth to be confusing, understand that $length \propto \mu$. So, apparent length $\propto$µ of the medium from which the image is viewed. The same applies for real length,
Real length $\propto$µ of medium in which object is present.
We always assume that the refractive index of air is 1, least mentioned.
The humblest way to approach the problem would be by understanding refractive indices. As the refractive index of water is greater than that of air, we would actually see the image of F at a closer distance than the actual depth. So, B will observe F, from a distance <6.8m. But the change will be tiny, not too huge. By this method we’ll arrive at option B.
Now using the same approach, we would actually see the image of B at a farther distance than the actual height, which leaves us with option C.