Question

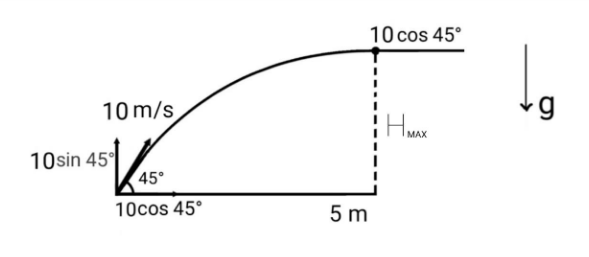
A fire extinguishing hose pipe disposes water at a speed of 10 m/s to put off fire on a building. Assuming a safe distance from the building on ground is 5 m, what is the maximum height at which water strikes the building?
(A) 1.75m
(B) 2.5m
(C) 3.75m
(D) 4.75m

Answer 1

Assume this question as a projectile motion question with initial velocity given as 10 meter per second and distance from the building will be half the total range along with maximum height at 45-degree angle.

Complete step by step answer:
This question can be treated as a projectile motion question where the water is being sprayed at an initial velocity of 10 meters per second and it must reach a building at 5 meters, with maximum height.

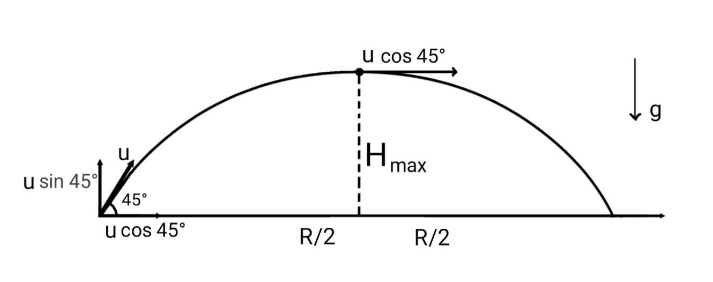
In projectile motion, the maximum height is attained when the initial velocity is projected at 45° angle and the distance from the point where the maximum height is reached to the point where the object is projected, is half of the total range of the motion. So,
For the projectile: -
$u = 10m{s^{ - 1}}$
$\theta = 45^\circ$
$\dfrac{R}{2} = 5$
$\therefore R = 10m$
We know that the motion is affected only by gravity, so everything has uniform acceleration of g towards the ground.

Now breaking the velocity vector into its two components, the horizontal and the vertical component.
Horizontal component: -
${u_{horizontal}} = u\cos 45^\circ = \dfrac{u}{{\sqrt 2 }} = \dfrac{{10}}{{\sqrt 2 }}m{s^{ - 1}}$
Vertical component: -
${u_{vertical}} = u\sin 45^\circ = \dfrac{u}{{\sqrt 2 }} = \dfrac{{10}}{{\sqrt 2 }}m{s^{ - 1}}$
Now, since it is accelerating only in vertical direction, we can use Newton’s 3rd equation in vertical direction to calculate the maximum height.
3rd equation: -
${v^2} = {u^2} + 2aS$
$v = 0,u = {u_{vertical}} = \dfrac{{10}}{{\sqrt 2 }},a = - g,S = {H_{\max }}$
$0 = {\left( {\dfrac{{10}}{{\sqrt 2 }}} \right)^2} + 2\left( { - g} \right){H_{\max }}$
$2g{H_{\max }} = \dfrac{{100}}{2}$
${H_{\max }} = \dfrac{{100}}{{4g}} = \dfrac{{25}}{g}$
taking $g = 10m{s^{ - 2}}$
${H_{\max }} = \dfrac{{25}}{{10}} = 2.5m$
Hence,option (B) is the correct answer.

Note: We assume water from the hose pipe as a projectile motion, but it isn't because water isn't a single particle, it is a complete stream of particles so the actual calculation might be different.