Question

A finger tip is pressed on a marble lying on a table in such a way that the marble is squeezed out from under the finger with the linear speed ${{v}_{0}}$ along the table simultaneously with a rotational speed ${{\omega }_{0}}$. The coefficient of sliding friction between the marble and the tabletop is $\mu$.
Then consider two cases:
Case (1) Marble is to slide and then come to a stop with linear and rotational motion reduced to zero at the same instant.
Case (2) Marble is to slide to a stop linearly but start return motion with a rotational speed of $\left( \dfrac{{{\omega }_{0}}}{2} \right)$.

A. For case (1), ${{v}_{0}}=\dfrac{1}{5}r{{\omega }_{0}}$
B. For the case (2), ${{v}_{0}}=\dfrac{1}{5}r{{\omega }_{0}}$
C. For the case (1), ${{v}_{0}}=\dfrac{2}{5}r{{\omega }_{0}}$
D. For the case (2), ${{v}_{0}}=\dfrac{2}{5}r{{\omega }_{0}}$

Answer 1

As a first step, you could make a free body diagram marking all the forces. Then you could apply an equation of motion for both rotational and sliding motion. You could then make necessary changes in these relations and then equate them each other accordingly in each case. Finally, you could get two relations of linear initial velocity with initial angular velocity.
Formula used:
Equation of motion,
$v={{v}_{0}}+at$
Moment of inertia of marble,
$I=\dfrac{2}{5}m{{r}^{2}}$

Complete answer:
In the question, we have a marble that is being squeezed out from under the finger with linear speed ${{v}_{0}}$ and a simultaneous rotational speed of${{\omega }_{0}}$. Let $\mu$ be the coefficient of sliding friction. We are also given two cases under this information.
Firstly, let us consider the free body diagram of the marble and then mark all the forces that are acting on it.

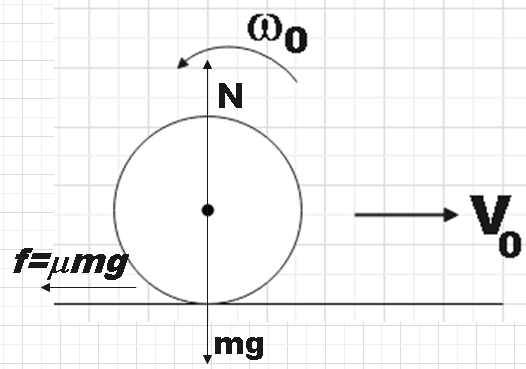
The force that is responsible for the sliding and rolling motion is frictional force.
From Newton’s equation of motion we have,
$v={{v}_{0}}+at$
But,
$F=ma=\mu mg$
$\Rightarrow a=\mu g$
$\therefore v={{v}_{0}}-\mu gt$ ………………………………………. (1)
Now for the rolling motion we have,
$\omega ={{\omega }_{0}}+\alpha t$
Where, $\alpha$ is the rotational acceleration.
We know that torque is given by,
$\tau =I\alpha =Fr$
$\Rightarrow \alpha =\dfrac{Fr}{I}=\dfrac{\mu mgr}{I}$
$\therefore \omega ={{\omega }_{0}}-\dfrac{\mu mgr}{I}t$ ……………………………………… (2)
(1) Now for the first case, final linear and angular velocity is zero. So equations (1) and (2) becomes,
$0={{v}_{0}}-\mu gt$
$\Rightarrow t=\dfrac{{{v}_{0}}}{\mu g}$ ………………………. (3)
$0={{\omega }_{0}}-\dfrac{\mu mgr}{I}t$
$\Rightarrow t=\dfrac{I{{\omega }_{0}}}{\mu mgr}$ …………………… (4)
From (3) and (4),
$\dfrac{{{v}_{0}}}{{{\omega }_{0}}}=\dfrac{I}{mr}$
Now for the moment of inertia marble,
$I=\dfrac{2}{5}m{{r}^{2}}$
$\Rightarrow \dfrac{{{v}_{0}}}{{{\omega }_{0}}}=\dfrac{\left( \dfrac{2}{5}m{{r}^{2}} \right)}{mr}$
$\therefore {{v}_{0}}=\dfrac{2}{5}r{{\omega }_{0}}$ …………………………………… (5)
(2) Now for the second case,$v=0$ and $\omega =\dfrac{{{\omega }_{0}}}{2}$
$\Rightarrow \dfrac{{{v}_{0}}}{\mu g}=\dfrac{I{{\omega }_{0}}}{2\mu mgr}$
$\Rightarrow {{v}_{0}}=\dfrac{\left( \dfrac{2}{5}m{{r}^{2}} \right)}{2mr}{{\omega }_{0}}$
$\therefore {{v}_{0}}=\dfrac{1}{5}r{{\omega }_{0}}$ ………………………………………………. (6)

Comparing equations (5) and (6) along with the given options in the question, we find that options B and C are the true conditions.

Note:
We are clearly given in the question that the body is going to rest after sliding in both the cases. So clearly we could conclude that the marble is undergoing decelerated motion. Therefore, we have assigned the sign for acceleration as negative as the velocity is being reduced over time.