Question
Question: (a) Find acceleration. (b) Find tension in the string.  Find acceleration.
(b) Find tension in the string.
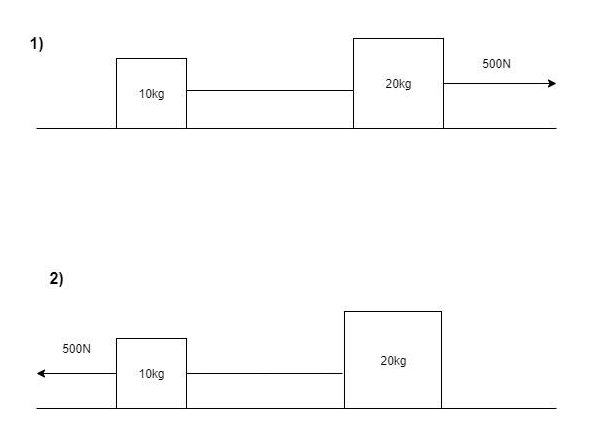
Solution
The force acting on a body creates acceleration. Now if the body attached to the string feels force, then, there originates a tension on the string. These tension pulls the body attached to the other end of the string and thus produces an acceleration to the whole system.
Step by step answer:
Formulae Used:
If a force F acts on an object of m and produces acceleration a then you have the expression
F=ma
Given:
For the figure (1):
The force F acted upon is 500N.
The mass of the immediately attached body is M=20kg.
The mass of the body attached to the other end is m=10kg.
For the figure (2):
The force F acted upon is 500N.
The mass of the immediately attached body is m=10kg.
The mass of the body attached to the other end is M=20kg.
To get: (a) The acceleration.
(b) The tension in the string.
Step 1:
Let the tension on the string be T. Let the acceleration on the system is a.
For the figure (1) you can equate the forces acting on the system.
500−T=20a
T=10a
Putting eq (3) in eq (2) you have
500−10a=20a ⇒30a=500 ⇒a=30500=16.67
∴a=16.67m/s2
So, calculate the value of T
T=16.67×10=166.7
∴T=166.7N
Step 2:
Let the tension on the string be T. Let the acceleration on the system is a.
For the figure (2) you can equate the forces acting on the system.
500−T=10a
T=20a
Putting eq (3) in eq (2) you have
500−20a=10a ⇒30a=500 ⇒a=30500=16.67
∴a=16.67m/s2
So, calculate the value of T
T=16.67×20=333.4
∴T=333.4N
Final Answer:
From figure (1),
a) The acceleration of the system is 16.67ms−2.
b) The tension on the string is 166.7N.
From figure (2),
a) The acceleration of the system is 16.67ms−2.
b) The tension on the string is 333.4N.
Note: The tension on the string plays a crucial role in the system. The end where the force is applied the tension on the string is generated. Similarly due to this tension a reaction is generated from the other end of the string. Here no friction is considered. So, you should take the acceleration of the whole system the same.
