Question

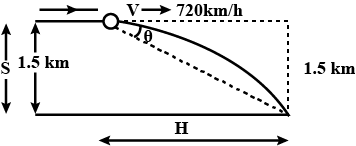
A fighter plane is flying horizontally at an altitude of 1.5 km with speed of 720 km/h. What angle of sight (w.r.t horizontal) when the target is seen, should the pilot drop the bomb in order to attack the target?
A) ${23^o}4'$
B) ${43^o}4'$
C) ${33^o}4'$
D) ${53^o}4'$

Answer 1

In these types of questions we follow the approach of Parabolic motion with the equation of motion in 2-D. We are going to break the motion in the x and y axis and then apply the equation of motion separately in horizontal and vertical motion.

Complete step by step answer:
Given is Vertical distance = S = 1.5 km
Speed=V=720km/h
The concept that we are to solve the question is as follows:
As clearly mentioned, the bomb will drop from the fighter plane so, when it leaves the plane at that instant its velocity becomes equal to the fighter jet. Hence, we can say at that instant the bomb will have only horizontal velocity and no vertical velocity.
As the time goes on it gains both horizontal and vertical velocity because of the presence of gravitational pull of acceleration $g$ but remember there is no acceleration in horizontal direction.
So concept is clear now and we will proceed to the solution-

Using formula of semi parabolic,
Time of flight
Let us discuss how get the formula of time of fight:
So, let consider the motion in vertical axis that is y-axis
Applying 3rd equation of motion
$h = ut + \dfrac{1}{2}g{t^2}$
Where u is the initial velocity in vertical direction, t is the time taken and h is the height.
$u = 0$
So, $h = \dfrac{1}{2}g{t^2}$

$= t = \sqrt {\dfrac{{2h}}{a}} {\text{ where a = g}} \\\ {\text{Then H = horizontal distance = }}vt = 720 \times \sqrt {\dfrac{{2 \times 1500}}{{9.8}}} = 3.5km \\\ {\text{So }}\tan \theta = \dfrac{{1.5}}{{3.5}} = 0.428 \\\ \theta = {\tan ^{ - 1}}0.428 = {23.17^o} \\\$

(tan$\theta$=$\dfrac{{{\text{perpendicular}}}}{{{\text{base}}}}$)

Hence the closest answer is ${23^o}4'$
So option (A) is correct

Note: The main point to remember here is units as most of the student converts km/h into m/s but forget to convert the final units into km/h due which fluctuation in answer occurs. secondly always remember the trigonometric formulas it will help you in the whole course. Also when it is said ‘drops’ in the question we assume the bomb is dropped with zero force and zero velocity in the y-direction.