Question

A fighter plane flying horizontally at an altitude of 1.5km with speed 720km/h passes directly overhead an anti-craft gun at what angle from the vertical should the gun be fired for the shell with muzzle speed 600m/s to hit the plane. At what minimum altitude should the plot fly the plane to avoid being hit? (Take $g=10m{{s}^{-2}}$).

Answer 1

In the above question it is given to us that the plane flies at an altitude of 1.5km. Hence we will first have to determine the time taken by the bullet to reach the height. Further we will consider a point at an altitude of 1.5km such that the distance covered by the plane from that point in time taken by the bullet to reach the same level is synchronized. Also we will obtain the maximum distance covered by the bullet along the vertical direction such that even if the bullet is shot at any angle it will not reach the plane.

Formula used:
$S=Ut-\dfrac{1}{2}g{{t}^{2}}$
${{V}^{2}}-{{U}^{2}}=-2gs$

Complete step by step answer:

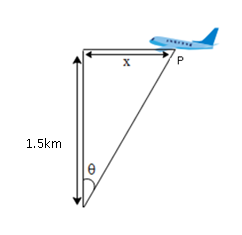
In the above figure we can see that the plane makes an angle $\theta$ with the vertical at point P. The plane flies at an altitude of 1.5km from the ground. So in order for the bullet from the anti-craft to basically hit the plane at this height. Hence from Newton’s second kinematic equation the time ‘t’ taken for the bullet to reach the height of S=1.5km is equal to,
$\begin{aligned} & S=Ut-\dfrac{1}{2}g{{t}^{2}}\text{, }\because U=600m/s \\\ & \Rightarrow 1500m=600t-\dfrac{1}{2}10{{t}^{2}} \\\ & \Rightarrow 300m=120t-{{t}^{2}} \\\ & \therefore {{t}^{2}}-120t+300=0 \\\ \end{aligned}$
Using the quadratic formula to solve the above equation we get,
$\begin{aligned} & {{t}^{2}}-120t+300=0 \\\ & \Rightarrow t=\dfrac{-(120)\pm \sqrt{{{120}^{2}}-4\times 1\times 300}}{2a} \\\ & \Rightarrow t=\dfrac{120\pm \sqrt{13200}}{2(1)}=\dfrac{120\pm 114.8}{2} \\\ & \therefore t=\dfrac{120+114.8}{2}=117.4\sec \text{ or,} \\\ & \therefore t=\dfrac{120-114.8}{2}=2.6\sec \\\ \end{aligned}$
Let us only consider the time taken for the bullet to reach the altitude of 1.5km as 2.6sec. Now let us say the plane is at some point P such that it takes 2.6 sec to reach the point where the bullet will hit it, We know the speed of the pane is 720km/h which is equal to 200m/s. Hence the distance(x) from point P to the point where the bullet hits the plane is equal to,
$\begin{aligned} & x=200m{{s}^{-1}}\times 2.6s \\\ & \therefore x=520m \\\ \end{aligned}$
Hence using the definition of tan of $\theta$ in the above figure we get,
$\begin{aligned} & \tan \theta =\dfrac{x}{1.5km} \\\ & \Rightarrow \tan \theta =\dfrac{520m}{1500m}=0.346 \\\ & \therefore \theta ={{19.1}^{\circ }} \\\ \end{aligned}$
Hence the angle made by the plane with the vertical should be ${{19.1}^{\circ }}$
If the plane basically flies at an altitude such that it is at maximum height where the bullet from the anti-craft can reach, the plane will never be hit by the bullet. In the above case it is given to us the bullet has a muzzle speed of i.e. its initial velocity is 600m/s and at maximum height its final velocity i.e. (V) is zero. Hence from Newton’s third kinematic equation we get the maximum height (s) reached by the bullet is equal to,
$\begin{aligned} & {{V}^{2}}-{{U}^{2}}=-2gs \\\ & \Rightarrow {{(0)}^{2}}-{{(600m{{s}^{-1}})}^{2}}=-2\times 10\times s \\\ & \Rightarrow \dfrac{360000}{20}=s \\\ & \therefore s=18000m \\\ \end{aligned}$
Therefore if the plane flies at a height of 18000m and above the plane will not be hit by the bullet of the anti-craft.

Note:
In the above question we basically obtained two values of time t. This is because the bullet will reach the same position at altitude of 1500m when it is going upwards and after some time when it’s basically coming downwards due to gravity. But in the above question I have only considered the first case as an anti craft usually hits the plane for the first time itself.