Question

A fighter plane flying horizontally at an altitude of 2km with a speed of 540km/h passes directly overhead an anti-aircraft gun. If the gun can fire a bullet at the muzzle speed of 500m/s, at what angle with the vertical should the gunfire so that the bullet hits the plane?
A. ${{\cos }^{-1}}\left( \dfrac{3}{10} \right)$
B. ${{\sin }^{-1}}\left( \dfrac{3}{10} \right)$
C. ${{\tan }^{-1}}\left( \dfrac{3}{10} \right)$
D. ${{\tan }^{-1}}\left( 1 \right)$

Answer 1

For a bullet fired at an angle θ with the vertical to hit the plane flying horizontally at some altitude, the horizontal distance covered by both bullet and plane should be equal. Resolve the given velocity vector into its horizontal and vertical components. Also, we know that distance covered at a given time is the product of the time and velocity, equating the distance covered by plane and bullet when the bullet hits the plane results in the horizontal component of the bullet being equal to the velocity of the plane. Hence, we get θ.
Formula used:
Distance covered at time t,
$x=v\times t$

Complete answer:

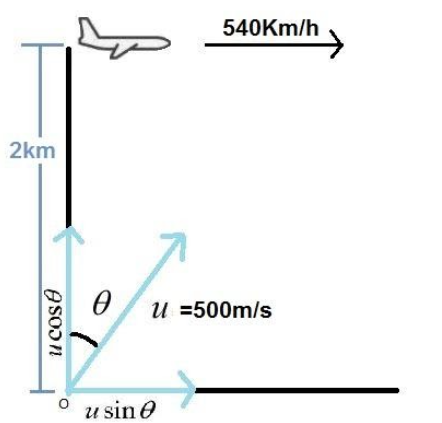
At the point ‘o’, an anti-aircraft gun is fired when a fighter plane moving at a speed of 540km/h passes directly overhead. And we are asked to find the angle at which it is fired so as to hit the fighter plane.
We are given the muzzle velocity of the gun, u= 500m/s.
We have to convert this value in units of km/h so as to make the calculation easier. $u=\left( 500m/s\times \dfrac{60\times 60}{1000} \right)km/h$
$u=1800km{{h}^{-1}}$
Now, we can resolve this velocity vector into its components. The horizontal and vertical components can be respectively given as,
${{u}_{v}}=u\cos \theta$
${{u}_{h}}=u\sin \theta$
In order for the bullet fired from the anti aircraft gun to hit the plane, the distance travelled by the plane at time ‘t’ should be equal to the horizontal distance covered by the bullet at the same time. The horizontal distance covered during the projectile motion of the bullet is also called its horizontal range.
Distance travelled by any object = velocity of the object × time taken
Therefore, at time t, when the bullet hits the plane,
Distance travelled by plane = horizontal range of the bullet in projectile motion
Let the velocity of plane be given by ‘v’ then,
$v\times t={{u}_{h}}\times t$
$v\times t=u\sin \theta \times t$
We are supposed to find angle θ, so rearranging the equations gives,
$\sin \theta =\dfrac{v}{u}$
We can now substitute the values, $\sin \theta =\dfrac{540km/h}{1800km/h}$
$\sin \theta =\dfrac{3}{10}$
$\theta ={{\sin }^{-1}}\left( \dfrac{3}{10} \right)$
So the answer is option B. The anti aircraft is to be fired at an angle${{\sin }^{-1}}\left( \dfrac{3}{10} \right)$ to hit the fighter plane.
Additional information:
Other important relations to be kept in mind while dealing with projectile motion with initial velocity ${{v}_{0}}$ and projectile angle θ are:
1. Time taken to reach the highest point,
${{t}_{peak}}=\dfrac{{{v}_{0}}\sin \theta }{g}$
2. Maximum height of a projectile,
${{y}_{peak}}=\dfrac{{{\left( {{v}_{0}}\sin \theta \right)}^{2}}}{2g}$
3. Maximum horizontal distance covered for a projectile,
${{x}_{\max }}=\dfrac{{{v}_{0}}^{2}\sin 2\theta }{g}$
4. Time taken for covering maximum horizontal distance,
${{t}_{xp}}=\dfrac{2{{v}_{0}}\sin \theta }{g}$

Note:
For any kinematics problem, drawing the figure as per the given conditions in the question will give you a clear idea about how to find the solution. Some given values in the question may not be required for finding the solution but may be given so as to divert us from a very simple solving method (eg:- 2km altitude given in this question).