Solveeit Logo
Login

Question

Question: A fighter plane flying horizontally at an altitude of \[1.5km\] with speed \(720km/h\) passes direct...

A fighter plane flying horizontally at an altitude of 1.5km1.5km with speed 720km/h720km/h passes directly overhead an anti-aircraft gun. At what angle from the vertical should the gun be fired for the shell with muzzle speed 600ms−1600ms^{-1} to hit the plane? At what minimum altitude should the pilot fly the plane to avoid being hit? (Take g=10ms−2g=10ms^{-2})

Explanation

Solution

Hint: This can be solved by the projectile motion where usin⁡θ=vtu \sin\theta=vt. Since the plane is already at certain height above the ground, we must check, the max height, till where the shell can reach Hmax=u2sin2(90−θ)2gH_{max}=\dfrac{u^{2}sin^{2}(90-\theta)}{2g}.

Formula used: usin⁡θ=vtu \sin\theta=vt
Hmax=u2sin2(90−θ)2gH_{max}=\dfrac{u^{2}sin^{2}(90-\theta)}{2g}

Complete step-by-step solution -
This is a projectile motion sum where,
Height of the fighter plane=1.5km=1500m1.5km=1500m
Speed of the plane v=720km/h=200m/sv=720km/h=200m/s
Let θ\theta be the angle, when the shell hits the plane.
Muzzle velocity u=600m/su=600m/s
Time taken to hit the plane=t=t
Horizontal distance travelled, from second equation of kinematic motion.=uxt=u_{x}t
Distance travelled by the plane=vt=vt

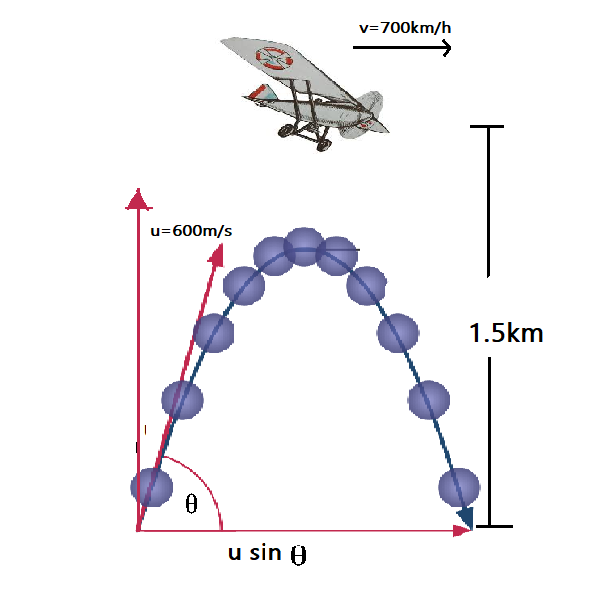
The shell will hit the plane if the above distances are equal.
uxt=vtu_{x}t=vt
usin⁡θ=vtu \sin\theta=vt
sin⁡θ=uv=200600=0.33\sin \theta=\dfrac{u}{v}=\dfrac{200}{600}=0.33
θ=sin⁡−1(0.33)≈19∘\theta=\sin^{-1}(0.33)\approx19^{\circ}
To avoid being hit, the plane must fly at Hmax=u2sin2(90−θ)2g=u2cos2θ2×10=6002cos21920=(600×0.945)220=16092=16kmH_{max}=\dfrac{u^{2}sin^{2}(90-\theta)}{2g}=\dfrac{u^{2}cos^{2}\theta}{2\times10}=\dfrac{600^{2}cos^{2}19}{20}=\dfrac{(600\times0.945)^{2}}{20}=16092=16km
Since it is already flying at 1.5km1.5km height it must fly above by another 16km16km to avoid being hit by the shell.

Note: Projectile motion occurs when an object is projected at a certain angle from the surface, it moves along a curved path called trajectory under the action of gravity. This curved path is of the shape of a parabola.
The various formulas used are
Time of flight=2v0sin⁡θg=\dfrac{2v_{0}\sin\theta}{g}
Maximum height Hmax=u2sin2(90−θ)2gH_{max}=\dfrac{u^{2}sin^{2}(90-\theta)}{2g}
Horizontal range R=u2sin2(90−θ)gR=\dfrac{u^{2}sin^{2}(90-\theta)}{g}
Where, v0v_{0} is the initial velocity, with sin⁡θ  ;cos⁡θ\sin\theta\;;\cos\theta as the y-axis and x-axis component respectively.