Question

A farmer wishes to grow a $100{{m}^{2}}$ rectangular vegetable garden. Since he has with the only 30m barbed wire, he fences three sides of the rectangular garden letting the compound wall of his house act as the fourth side – fence. Find the dimensions of his garden.

Answer 1

Hint: Find the perimeter of the fence in which one side is kept open and substitute these values to the area of the rectangle. Solve the quadratic equation formed. Thus find the dimensions of the rectangle.

Complete step by step answer:
We have been given the area of the rectangular vegetable garden as $100{{m}^{2}}$. We need to find the dimensions of his garden.

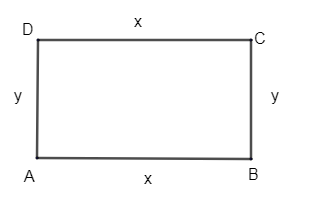
Let us take ‘x’ as the length of the rectangular vegetable garden and ‘y’ as its breadth.
It is said that he has only 30m barbed wire, which he fences three sides . Thus, taking the perimeters of the rectangle of three sides and ${{4}^{th}}$ side open. Let us assume that side AD is the ${{4}^{th}}$ fence.
$\therefore$ Perimeter = CD + BC + AB = 30m.
From the figure,
x + y +x = 30
$\therefore$ y = 30 – 2x
The area of the rectangular garden = $100{{m}^{2}}$.
$\therefore$ xy = 100.
Put the value of y = 30 – 2x.
$\therefore$ x (30 – 2x) = 100

& 30x-2{{x}^{2}}=100 \\\ & \therefore 2{{x}^{2}}-30x+100=0 \\\ \end{aligned}$$ Divide the entire equation by 2. $$\therefore {{x}^{2}}-15x+50=0-(1)$$ The above equation is similar to a quadratic equation whose general form is $$a{{x}^{2}}+bx+c=0$$. By comparing both equation (1) and general equation we get, a = 1, b = -15, c = 50. Thus substituting these values in the quadratic formula, $$\begin{aligned} & \dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}=\dfrac{-\left( -15 \right)\pm \sqrt{{{\left( -15 \right)}^{2}}-4\times 1\times 50}}{2\times 1} \\\ & =\dfrac{15\pm \sqrt{225-200}}{2}=\dfrac{15\pm \sqrt{25}}{2}=\dfrac{15\pm 5}{2} \\\ \end{aligned}$$ Thus the roots are $$\left( \dfrac{15+5}{2} \right)$$ and $$\left( \dfrac{15-5}{2} \right)$$ = 10 and 5. If we take x = 5, then, $$y=30-2x=30-2\times 5=20$$ m. If we take, x = 10, then, $$y=30-2\times 10=10$$ m. Thus the dimensions of a vegetable garden can be either 5m $$\times $$ 20m or it can be 10m $$\times $$ 10m. Hence we got the required dimensions. Note: We know that perimeter is the total length of the closed figure. Thus add all the sides. But here the 30m wire can cover only 3 sides, so the perimeter of $${{4}^{th}}$$ side is not added. Thus the perimeter will be (x + y + x) i.e. their total will be 30m.Students should remember the formula of finding roots of quadratic equation and basic formulas of geometric figure rectangle. .