Question

A farmer moves along the boundary of a square field of side 10m in 40s. What will be the magnitude of displacement of the farmer at the end of 2minutes 20seconds?

Answer 1

From the given side length of the square field, we could find its perimeter. The distance covered by the farmer when he goes one round around the field will be the perimeter and we are given the time taken for that as 40s and hence we will get the speed of the farmer. Using this speed we could find the distance covered in 2min 20s. Then find the displacement accordingly.

Formula used: Distance-speed relation,
$v=\dfrac{d}{t}$

Complete step by step answer:
In the question, we are given that a farmer is moving along the boundary of a square field whose side is 10min in 40s. From this given information, we are asked to find the displacement of the farmer at the end of 2minutes and 20seconds.
Perimeter of the square of side ‘a’ is given by 4a
So the perimeter of side 10m will be,
$P=4\times 10=40m$
Total time taken by the farmer to go one round around the boundary of this field is,
$t=40s$
We know the relation between distance (d), speed (v) and time taken (t) given by,
$v=\dfrac{d}{t}$………………………………………… (1)
The distance covered here is the perimeter of the square, so, the speed will be,
$v=\dfrac{40}{40}=1m{{s}^{-1}}$
But we are asked to find the magnitude of displacement,
$t=120+20=140s$
Again, we could use equation (1) to get the answer.
$d=v\times t$
$\Rightarrow d=1\times 140m$
$\therefore d=140m$
So if the total distance covered is 140m, the total number of times the farmer went around the field will be,
$n=\dfrac{140}{40}=3.5$

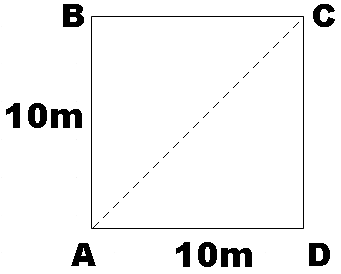
So if we consider the point A as the origin point from where the farmer starts to go around the field, then, on completing 140m he would have came back to point and travelled half the perimeter again. So at the he would be at point C.
Now the displacement of the farmer from the origin now will be the diagonal of the square field,
$s=\sqrt{{{10}^{2}}+{{10}^{2}}}m$
$\therefore s=14.14m$

Hence, we found the magnitude of displacement of the farmer at the end of 2minutes 20seconds to be 14.14m.

Note: We know that distance covered by the body is very different from the displacement of the body. Displacement if a vector quantity while displacement is a vector quantity. By distance, we mean the ground covered by any object or person and displacement between two points is the shortest distance between those points.