Question

A farmer has 10 acres of land to plant wheat and rye. He has to plant at-least 7 acres. Each acre of wheat costs Rs. 200 and each acre of rye costs Rs. 100 to plant. He has only Rs. 1200 to spend. Moreover, the farmer has to get the planting done in 12 hours and it takes 1 hour to plant an acre of wheat and 2 hours to plant an acre of rye. An acre of wheat yields a profit of Rs. 500 and an acre of rye yields a profit of Rs. 300.
(Take x and y as the acres of wheat and rye planted respectively). What is the maximum profit that the farmer can make?

Answer 1

According to the question given in the question we have to determine the maximum profit that the farmer can make so when a farmer has 10 acres of land to plant wheat and rye. He has to plant at-least 7 acres. Each acre of wheat costs Rs.200 and each acre of rye costs Rs. 100 to plant. He has only Rs. 1200 to spend. Moreover, the farmer has to get the planting done in 12 hours and it takes 1 hour to plant an acre of wheat and 2 hours to plant an acre of rye. An acre of wheat yields a profit of Rs. 500 and an acre of rye yields a profit of Rs. 300. So, first of all we have to count the number of acres for wheat and rye plants.
Now, we have to obtain a linear expression as mentioned that at-least 7 acres is to be planted.
Now, we have to determine the total cost of planting the acres of wheat as we let and the same as we have to determine the cost of planting the acres of rye as we let.
Now, as mentioned that the total cost of planting wheat and rye is Rs. 1200 so, we have to obtain the expression for the cost price of wheat and rye.
Now, as mentioned in the question that time taken to plant 1 acre of field is 1 hour so, we have to determine the time take to plant x acres and same as mentioned that the time taken to plant the rye is 2 hours so, we have to determine the time taken to plant the acres of rye.
Now, as mentioned that the total timing for planting is 12 hours so, we have to obtain the linear expression for planting time of wheat and rye.
Now, we have to determine the profit for the x acres of the wheat and the same as the profit for y acres of rye and obtain a linear equation.
Now, we have to draw the graph for all of the linear equations to obtain all the points and then we have to substitute all the points in the expression to obtain the required solution

Complete step-by-step answer:
Step 1: First of all we have to let the number of acres for wheat and rye plant as mentioned in the solution hint. Hence,
Let, x be the acres of wheat planted and y be the acres of rye planted.
Step 2: Now, we have to obtain a linear expression as mentioned that at-least 7 acres is to be planted as mentioned in the solution hint. Hence,
$\Rightarrow x + y \geqslant 7$……………………(1)
Step 3: Now, we have to determine the total cost of planting of the acres of wheat as we let and same as we have to determine the cost of planting of the acres of rye as we let,
As we know that cost of planting of 1 acre of wheat is Rs. 200
So, the cost of planting of x acres of wheat is Rs. 200x
Same as,
As we know that cost of planting of 1 acre of rye is Rs. 100
So, the cost of planting of x acres of rye is Rs. 100x
Step 4: Now, as mentioned that the total cost of planting wheat and rye is Rs. 1200 so, we have to obtain the expression for the cost price of wheat and rye. Hence, total cost of planting wheat and rye,
$\Rightarrow 200x + 100y \leqslant 1200 \\\ \Rightarrow 2x + y \leqslant 12........................(2) \\\$
Step 5: Now, as mentioned in the question that time taken to plant 1 acre of field is 1 hour so, we have to determine the time take to plant x acres and same as mentioned that the time taken to plant the rye is 2 hours so, we have to determine the time taken to plant the acres of rye. Hence,
Time taken to plant 1 acre of wheat $= 1hr$
So, Time taken to plant x acre of wheat$= xhr$
Same as,
Time taken to plant 1 acre of rye $= 2hr$
So, Time taken to plant x acre of rye$= 2xhr$
Step 6: Now, as mentioned that the total timing for planting is 12 hours so, we have to obtain the linear expression for planting time of wheat and rye as mentioned in the solution hint. Hence,
$\Rightarrow x + 2y \leqslant 12$…………………..(3)
Step 7: Now, we have to determine the profit for yielding the field as below:
1 acres of wheat yields a profit of $= Rs. 500$
So, x acres of wheat yields a profit of$= Rs. 500x$
Same as,
1 acres of rye yields a profit of$= Rs. 300$
So, x acres of rye yields a profit of$= Rs. 300y$
Step 8: Now, we have to determine the profit for the x acres of the wheat and same as the profit for y acres of rye and obtain a linear equation.
$\Rightarrow P = 500x + 300y....................(4)$
Step 9: Now, we have to make a graph to obtain all the points with the help of the expression (1), (2), and (3) as obtained in the previous solution steps. Hence,

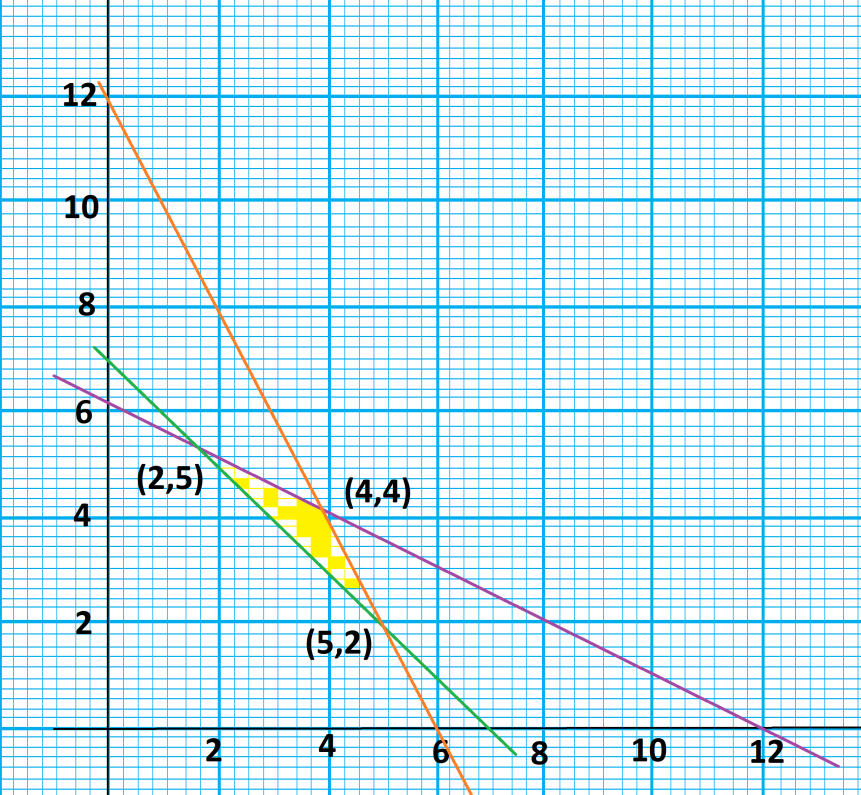
Step 10: Now, we have to substitute all the points as obtained in the graph as in the expression (4) hence,
On substituting all the points in the expression (4),
Substituting (4,4),
$\Rightarrow P = 500(4) + 300(4) \\\ \Rightarrow P = 2000 + 1200 \\\ \Rightarrow P = 3200 \\\$
Substituting (2,5),
$\Rightarrow P = 500(2) + 300(5) \\\ \Rightarrow P = 1000 + 1500 \\\ \Rightarrow P = 2500 \\\$
Substituting (5,2),
$\Rightarrow P = 500(5) + 300(2) \\\ \Rightarrow P = 2500 + 600 \\\ \Rightarrow P = 3100 \\\$
Hence, as we can see that Rs. 3200 is the maximum profit.

Final solution: Hence, with the help of the graph we have determined the maximum profit which is Rs. 3200 can be done by the farmer.

Note:
It is necessary to draw the graph for all of the linear equations to obtain all the points and then we have to substitute all the points in the expression to obtain the required solution.
To determine the profit for the x acres of the wheat and same as the profit for y acres of rye and obtain a linear equation as well as for the other information.