Question

A farmer has 10 acres of land to plant wheat and rye. He has to plant at least 7 acres. Each acre of wheat costs {}$200 and each acre of rye costs${}100 to plant. He has only {}$1200 to spend. Moreover, the farmer has to get the planting done in 12 hours and it takes 1 hour to plant an acre of wheat and 2 hours to plant an acre of rye. An acre of wheat yields a profit of${}500 and an acre of rye yields a profit of {}$300. (Take x and y as the acres of wheat and rye planted respectively). What is the maximum profit that the farmer can make? A.${}2500
B. {}$2800 C.${}3100
D. {}$3200

Answer 1

Proceed the solution by making the linear equation in two variables which is formed using the question’s information. This concept will help you on the right track to reach the answer. In this question, the number of acres of wheat planted and acres of rye planted is variable so we can make an equation in terms of that.

Complete step-by-step answer:
Let x be the acres of wheat planted and y be the acres of rye planted

Given that there are a total of 10 acres of land to plant.
At least 7 acres is to be planted
Hence we can form linear equation in two variables as
⟹x+y ≥ 7 ……… (1)

Given that the cost to plant one acre of wheat is {}$200
Therefore, the cost for x acres of wheat can be find by unitary method and it will be equal to 200x

Given that the cost to plant one acre of rye is {}$100
Therefore, the cost for y acres of rye can be find by unitary method and it will be equal to 100y

Given that, an amount for planting wheat and rye is {}$1200 the total cost to plant wheat and rye is 200x+100y which will be equal to${}1200

Therefore, in equation form we can write
The total cost to plant wheat and rye is 200x+100y≤1200
On simplifying
⟹2x+y≤12 ………… (2)

Given that, the time taken to plant one acre of wheat is 1 hr
Therefore, using unitary method
the time taken to plant x acres of wheat is x hrs

Given that, the time taken to plant one acre of rye is 2 hrs
Therefore, using unitary method
the time taken to plant y acres of rye is 2y hrs

Given that, the total time for planting is 12 hrs
Therefore, the total time to plant wheat and rye is x+2y≤12 ………. (3)

Given that, one acre of wheat yields a profit of {}$500
Therefore, the profit from x acres of wheat is 500x

Given that, one acre of rye yields a profit of {}$300
Therefore, the profit from y acres of wheat is 300y
therefore,
the total profit(P) from the wheat and rye is P =500x+300y ………… (4)

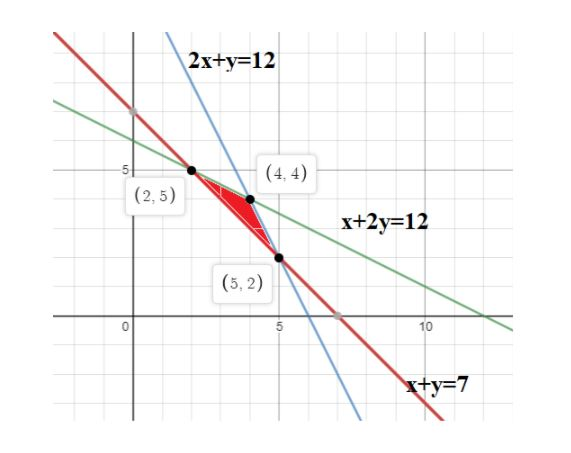
In the above figure, the red shaded region is the feasible region with three corner points. (4,4), (2,5), (5,2)
Now substituting the corner points, the profit equation,
substituting (4,4)
The total profit(P) from the wheat and rye is P =500x+300y
⟹ Total profit(P)=500x+300y=500(4)+300(4)=3200

substituting (2,5)
The total profit(P) from the wheat and rye is P =500x+300y
⟹ Total profit(P)=500x+300y=500(2)+300(5)=2500

substituting (5,2)
The total profit(P) from the wheat and rye is P =500x+300y
⟹ Total profit(P)=500x+300y=500(5) +300(2) =3100
Hence we got maximum value of profit on substituting (4,4), it means when a farmer planted 4 acres of wheat and 4 acres of rye then he would have got maximum profit.

So, the correct answer is “Option D”.

Note: In this particular problem farmer seeks to maximize his profit which is a known function, subject to a set of linear constraints on the function. Linear Programming Problems (LPP) provide the method of finding such an optimized function along with the values which would optimize the required function accordingly.