Question

A family of chords of the parabola ${{y}^{2}}=4ax$ is drawn so that their projections on a straight line inclined equally to both the axes are all of a constant length c; prove that the locus of their middle point is the curve $\left( {{y}^{2}}-4ax \right){{\left( y+2a \right)}^{2}}+2{{a}^{2}}{{c}^{2}}=0$.

Answer 1

Let us assume the two parametric coordinates on the parabola $\left( a{{t}_{1}}^{2},2a{{t}_{1}} \right)\And \left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)$ and join them to make a chord. After that assume the midpoint of these two coordinates as (h, k) and write the midpoint of x coordinates and equate it to h, similarly write the midpoint of the coordinates of y and equate it to k. Solve these two equations and build some relations. It is given that the straight line on which projections of the chord have occurred is equally inclined to x and y axes; this means the equation for this straight line is $y=x$. Draw this line on the parabola and after that using the basic geometry by dropping the perpendiculars from the two parametric coordinates onto the straight line $y=x$ find the relation between h and k. And locus is found by replacing these h and k by x and y respectively.

Complete step-by-step answer:
We have given a parabola as follows:
${{y}^{2}}=4ax$
Now, we are drawing a parabola ${{y}^{2}}=4ax$ along with the chord on this parabola having parametric coordinates as $\left( a{{t}_{1}}^{2},2a{{t}_{1}} \right)\And \left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)$.

Let us suppose the midpoint of this chord AB as (h, k) so we are drawing this midpoint on the chord AB.

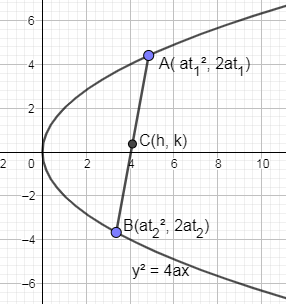
Now, we are going to write the midpoint of AB in terms ${{t}_{1}}\And {{t}_{2}}$ we get,
$\begin{aligned} & h=\dfrac{a{{t}_{1}}^{2}+a{{t}_{2}}^{2}}{2} \\\ & k=\dfrac{2a{{t}_{1}}+2a{{t}_{2}}}{2} \\\ \end{aligned}$
Simplifying the above relations we get,
$\begin{aligned} & 2h=a\left( {{t}_{1}}^{2}+{{t}_{2}}^{2} \right)........Eq.(1) \\\ & 2k=2a\left( {{t}_{1}}+{{t}_{2}} \right)..........Eq.(2) \\\ \end{aligned}$
Squaring on both the sides of the above equation we get,
$\begin{aligned} & {{k}^{2}}={{a}^{2}}{{\left( {{t}_{1}}+{{t}_{2}} \right)}^{2}} \\\ & \Rightarrow {{k}^{2}}={{a}^{2}}\left( {{t}_{1}}^{2}+{{t}_{2}}^{2}+2{{t}_{1}}{{t}_{2}} \right) \\\ \end{aligned}$
Using eq. (1) in the above equation we get,
$\begin{aligned} & {{k}^{2}}={{a}^{2}}\left( \dfrac{2h}{a}+2{{t}_{1}}{{t}_{2}} \right) \\\ & \Rightarrow {{k}^{2}}=2ha+2{{a}^{2}}{{t}_{1}}{{t}_{2}} \\\ & \Rightarrow {{t}_{1}}{{t}_{2}}=\dfrac{{{k}^{2}}-2ha}{2{{a}^{2}}}.......Eq.(3) \\\ \end{aligned}$
In the above problem, we have given that the family of chords is projected on a line which is equally inclined to x and y axes and the length of projection is c.
We know that, equation of a line which is equally inclined to x and y axes are equal to:
$\begin{aligned} & y=x \\\ & \Rightarrow x-y=0 \\\ \end{aligned}$
Now, drawing the above line on the parabola we get,

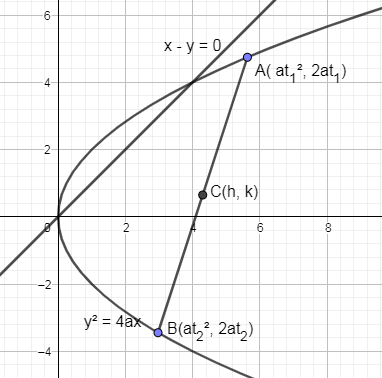
Let us drop a perpendicular on the line $x-y=0$ from points A and B we get,

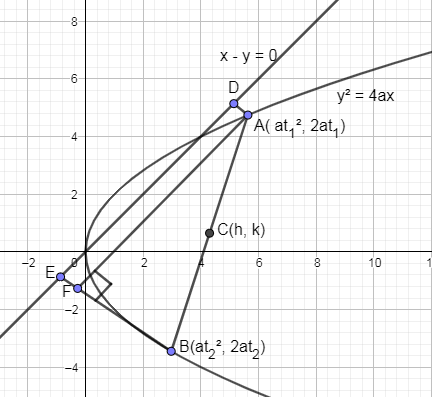
As you can see from the above figure that we have dropped perpendicular from point A as AD on $x-y=0$ and from point B we have dropped a perpendicular BE on$x-y=0$. ED is the projection of the chords onto the line $x-y=0$ and it is given as c.
Now, we are going to find the perpendicular distance from point A on $x-y=0$ by using the following formula:
We know that, the perpendicular distance from point $P\left( {{x}_{1}},{{y}_{1}} \right)$ to the line $ax+by+c=0$ is calculated using the following formula:
$\dfrac{a{{x}_{1}}+b{{y}_{1}}+c}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$
The perpendicular distance AD is equal to:
$\begin{aligned} & \dfrac{a{{t}_{1}}^{2}-2a{{t}_{1}}}{\sqrt{{{1}^{2}}+{{1}^{2}}}} \\\ & =\dfrac{a{{t}_{1}}^{2}-2a{{t}_{1}}}{\sqrt{2}} \\\ \end{aligned}$
Similarly, we are going to calculate the perpendicular distance from point B to $x-y=0$ which is equal to BE.
$BE=\dfrac{a{{t}_{2}}^{2}-2a{{t}_{2}}}{\sqrt{2}}$
And if you see the figure, you will find that $AD=FE$ so the length of FE is equal to:
$\dfrac{a{{t}_{1}}^{2}-2a{{t}_{1}}}{\sqrt{2}}$
The length of BF is equal to the difference of BE and FE.
$\begin{aligned} & \dfrac{a{{t}_{2}}^{2}-2a{{t}_{2}}}{\sqrt{2}}-\dfrac{a{{t}_{1}}^{2}-2a{{t}_{1}}}{\sqrt{2}} \\\ & =\dfrac{a{{t}_{2}}^{2}-2a{{t}_{2}}-\left( a{{t}_{1}}^{2}-2a{{t}_{1}} \right)}{\sqrt{2}} \\\ & =\dfrac{a{{t}_{2}}^{2}-2a{{t}_{2}}-a{{t}_{1}}^{2}+2a{{t}_{1}}}{\sqrt{2}} \\\ & =\dfrac{a\left( {{t}_{2}}^{2}-{{t}_{1}}^{2} \right)-2a\left( {{t}_{2}}-{{t}_{1}} \right)}{\sqrt{2}} \\\ & =\dfrac{a\left( {{t}_{2}}-{{t}_{1}} \right)\left( {{t}_{2}}+{{t}_{1}} \right)-2a\left( {{t}_{2}}-{{t}_{1}} \right)}{\sqrt{2}} \\\ \end{aligned}$
Taking $a\left( {{t}_{2}}-{{t}_{1}} \right)$ as common from the above expression we get,
$\dfrac{a\left( {{t}_{2}}-{{t}_{1}} \right)\left( {{t}_{2}}+{{t}_{1}}-2 \right)}{\sqrt{2}}$
Hence, we got the length of BF as:
$\dfrac{a\left( {{t}_{2}}-{{t}_{1}} \right)\left( {{t}_{2}}+{{t}_{1}}-2 \right)}{\sqrt{2}}$
As you can see that $\Delta AFB$ is a right angled triangle and we know the length of BF, length of AF is equal to DE which is equal to c and length of AB we can calculate by distance formula.
The length of AB is calculated as follows:
$\begin{aligned} & \sqrt{{{\left( a{{t}_{2}}^{2}-a{{t}_{1}}^{2} \right)}^{2}}+{{\left( 2a{{t}_{2}}-2a{{t}_{1}} \right)}^{2}}} \\\ & =\sqrt{{{a}^{2}}{{\left( {{t}_{2}}^{2}-{{t}_{1}}^{2} \right)}^{2}}+4{{a}^{2}}{{\left( {{t}_{2}}-{{t}_{1}} \right)}^{2}}} \\\ \end{aligned}$
Taking ${{a}^{2}}$ out from the square root we get,
$\begin{aligned} & a\sqrt{{{\left( {{t}_{2}}^{2}-{{t}_{1}}^{2} \right)}^{2}}+4{{\left( {{t}_{2}}-{{t}_{1}} \right)}^{2}}} \\\ & =a\sqrt{{{\left( {{t}_{2}}-{{t}_{1}} \right)}^{2}}{{\left( {{t}_{2}}+{{t}_{1}} \right)}^{2}}+4{{\left( {{t}_{2}}-{{t}_{1}} \right)}^{2}}} \\\ \end{aligned}$
Now, we are using the Pythagoras theorem in $\Delta AFB$ which is equal to:
${{\left( Hypotenuse \right)}^{2}}={{\left( Perpendicular \right)}^{2}}+{{\left( Base \right)}^{2}}$
Substituting hypotenuse, perpendicular and base as AB, AF and BF respectively in the above equation we get,
${{\left( AB \right)}^{2}}={{\left( AF \right)}^{2}}+{{\left( BF \right)}^{2}}$
$\begin{aligned} & {{\left( a\sqrt{{{\left( {{t}_{2}}-{{t}_{1}} \right)}^{2}}{{\left( {{t}_{2}}+{{t}_{1}} \right)}^{2}}+4{{\left( {{t}_{2}}-{{t}_{1}} \right)}^{2}}} \right)}^{2}}={{c}^{2}}+{{\left( \dfrac{a\left( {{t}_{2}}-{{t}_{1}} \right)\left( {{t}_{2}}+{{t}_{1}}-2 \right)}{\sqrt{2}} \right)}^{2}} \\\ & \Rightarrow {{a}^{2}}\left[ {{\left( {{t}_{2}}-{{t}_{1}} \right)}^{2}}{{\left( {{t}_{2}}+{{t}_{1}} \right)}^{2}}+4{{\left( {{t}_{2}}-{{t}_{1}} \right)}^{2}} \right]={{c}^{2}}+\dfrac{{{a}^{2}}{{\left( {{t}_{2}}-{{t}_{1}} \right)}^{2}}{{\left( {{t}_{2}}+{{t}_{1}}-2 \right)}^{2}}}{2}........Eq.(4) \\\ \end{aligned}$
We know the value of ${{\left( {{t}_{2}}+{{t}_{1}} \right)}^{2}}$ and require the value of ${{\left( {{t}_{2}}-{{t}_{1}} \right)}^{2}}$.
We are going to evaluate ${{\left( {{t}_{2}}-{{t}_{1}} \right)}^{2}}$ as follows:
$\begin{aligned} & {{\left( {{t}_{2}}-{{t}_{1}} \right)}^{2}}={{\left( {{t}_{2}}+{{t}_{1}} \right)}^{2}}-4{{t}_{2}}{{t}_{1}} \\\ & \Rightarrow {{\left( {{t}_{2}}-{{t}_{1}} \right)}^{2}}=\dfrac{{{k}^{2}}}{{{a}^{2}}}-4\left( \dfrac{{{k}^{2}}-2ha}{2{{a}^{2}}} \right) \\\ \end{aligned}$
$\begin{aligned} & \Rightarrow {{\left( {{t}_{2}}-{{t}_{1}} \right)}^{2}}=\dfrac{2{{k}^{2}}-4{{k}^{2}}+8ha}{2{{a}^{2}}} \\\ & \Rightarrow {{\left( {{t}_{2}}-{{t}_{1}} \right)}^{2}}=\dfrac{8ha-2{{k}^{2}}}{2{{a}^{2}}} \\\ & \Rightarrow {{\left( {{t}_{2}}-{{t}_{1}} \right)}^{2}}=\dfrac{4ha-{{k}^{2}}}{{{a}^{2}}} \\\ \end{aligned}$
Substituting the above value in eq. (4) we get,
$\begin{aligned} & {{a}^{2}}\left[ \dfrac{4ha-{{k}^{2}}}{{{a}^{2}}}{{\left( \dfrac{k}{a} \right)}^{2}}+4\dfrac{4ha-{{k}^{2}}}{{{a}^{2}}} \right]={{c}^{2}}+\dfrac{{{a}^{2}}\left( \dfrac{4ha-{{k}^{2}}}{{{a}^{2}}} \right){{\left( \dfrac{k}{a}-2 \right)}^{2}}}{2} \\\ & \Rightarrow {{a}^{2}}\left( \dfrac{4ha-{{k}^{2}}}{{{a}^{2}}} \right)\left[ \dfrac{{{k}^{2}}}{{{a}^{2}}}+4 \right]={{c}^{2}}+\dfrac{4ha-{{k}^{2}}}{2}{{\left( \dfrac{k-2a}{a} \right)}^{2}} \\\ & \Rightarrow \left( 4ha-{{k}^{2}} \right)\left( \dfrac{{{k}^{2}}+4{{a}^{2}}}{{{a}^{2}}} \right)=\dfrac{2{{a}^{2}}{{c}^{2}}+\left( 4ha-{{k}^{2}} \right){{\left( k-2a \right)}^{2}}}{2{{a}^{2}}} \\\ \end{aligned}$
In the above equation, $\dfrac{1}{{{a}^{2}}}$ will be cancelled from both the sides we get,
$\begin{aligned} & \left( 4ha-{{k}^{2}} \right)\left( \dfrac{{{k}^{2}}+4{{a}^{2}}}{1} \right)=\dfrac{2{{a}^{2}}{{c}^{2}}+\left( 4ha-{{k}^{2}} \right){{\left( k-2a \right)}^{2}}}{2} \\\ & \Rightarrow 2\left( 4ha-{{k}^{2}} \right)\left( {{k}^{2}}+4{{a}^{2}} \right)=2{{a}^{2}}{{c}^{2}}+\left( 4ha-{{k}^{2}} \right){{\left( k-2a \right)}^{2}} \\\ & \Rightarrow \left( 4ha-{{k}^{2}} \right){{\left( k-2a \right)}^{2}}-2\left( 4ha-{{k}^{2}} \right)\left( {{k}^{2}}+4{{a}^{2}} \right)+2{{a}^{2}}{{c}^{2}}=0 \\\ \end{aligned}$
Rearranging the above equation will give:
$\left( {{k}^{2}}-4ah \right){{\left( k+2a \right)}^{2}}+2{{a}^{2}}{{c}^{2}}=0$
Substituting h as x and k as y in the above equation will give the locus.
$\left( {{y}^{2}}-4ax \right){{\left( y+2a \right)}^{2}}+2{{a}^{2}}{{c}^{2}}=0$
Hence, we have shown that the locus of the middle point of the family of chords is $\left( {{y}^{2}}-4ax \right){{\left( y+2a \right)}^{2}}+2{{a}^{2}}{{c}^{2}}=0$.

Note: The most plausible mistake in the above problem is the calculation mistake which is clearly seen from the rigorous calculations. Apart from that there is also a place where the mistake could most likely occur is as follows:
When we have calculated the value of ${{\left( {{t}_{2}}-{{t}_{1}} \right)}^{2}}$ in the above problem as follows:
$\begin{aligned} & {{\left( {{t}_{2}}-{{t}_{1}} \right)}^{2}}={{\left( {{t}_{2}}+{{t}_{1}} \right)}^{2}}-4{{t}_{2}}{{t}_{1}} \\\ & \Rightarrow {{\left( {{t}_{2}}-{{t}_{1}} \right)}^{2}}=\dfrac{{{k}^{2}}}{{{a}^{2}}}-4\left( \dfrac{{{k}^{2}}-2ha}{2{{a}^{2}}} \right) \\\ \end{aligned}$
Now, in the above calculations you might subtract $2{{t}_{1}}{{t}_{2}}$ from ${{\left( {{t}_{1}}+{{t}_{2}} \right)}^{2}}$ which will make the expression look like:
${{\left( {{t}_{2}}-{{t}_{1}} \right)}^{2}}={{\left( {{t}_{2}}+{{t}_{1}} \right)}^{2}}-2{{t}_{2}}{{t}_{1}}$
To avoid this mistake, you can check the L.H.S and R.H.S of the above equation.
$\begin{aligned} & {{t}_{2}}^{2}+{{t}_{1}}^{2}-2{{t}_{1}}{{t}_{2}}={{t}_{2}}^{2}+{{t}_{1}}^{2}+2{{t}_{1}}{{t}_{2}}-2{{t}_{1}}{{t}_{2}} \\\ & \Rightarrow {{t}_{2}}^{2}+{{t}_{1}}^{2}-2{{t}_{1}}{{t}_{2}}={{t}_{2}}^{2}+{{t}_{1}}^{2}+0 \\\ & \Rightarrow {{t}_{2}}^{2}+{{t}_{1}}^{2}-2{{t}_{1}}{{t}_{2}}={{t}_{2}}^{2}+{{t}_{1}}^{2} \\\ \end{aligned}$
As you can see that L.H.S is not coming equal to R.H.S so that means we have wrongly written the above expression and here you will quickly spot your mistake and correct it.