Question

A fair coin is tossed 30 times. What is the probability that the coin will show heads fewer than 17 times?

Answer 1

To solve this question, we need to use the method of Binomial approximation. We calculate the mean and standard deviation. Using these values, we find the z value, which is required to refer to the area under the normal distribution table to calculate the probability values.

Complete step-by-step answer:
We can use this Binomial Approximation method to solve this problem. We can use this normal distribution as an approximation to binomial distribution only under certain conditions such as,
The sample size being large (n is large).
The probability given should be close to 0.5 (p is close to 0.5).
Given data:
The sample size n is 30.
Probability of heads occurring p is 0.5.
Probability of no heads occurring (tails occurring) q is,
$\begin{aligned} & \Rightarrow 1-p \\\ & \Rightarrow 1-0.5 \\\ \end{aligned}$
Probability of no heads occurring q is 0.5.
We need to calculate the mean as follows:
We know Mean is given by $\overline{x}=np.$
$\begin{aligned} & \Rightarrow \overline{x}=30\times 0.5 \\\ & \Rightarrow \overline{x}=15 \\\ \end{aligned}$
We know that the standard deviation is given by the formula,
$\sigma =\sqrt{npq}$
Therefore, we can calculate this standard deviation as,
$\begin{aligned} & \Rightarrow \sigma =\sqrt{30\times 0.5\times 0.5} \\\ & \Rightarrow \sigma =2.7386 \\\ \end{aligned}$
To calculate the z value, we use the formula $z=\dfrac{x-\overline{x}}{\sigma }.$
Here x is the number of desired heads which in this case is less than 17. The number less than 17 is 16. Hence, x is 16.
$\Rightarrow z=\dfrac{16-15}{2.7386}$
$\Rightarrow z=0.3652$
We can approximate this z value as 0.37.
We now refer to the table known as Binomial approximation table which represents the probability values for the given z values.

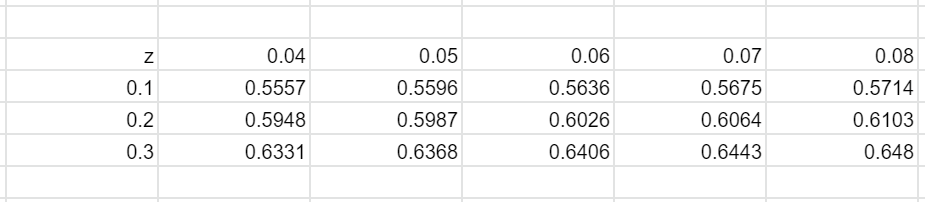
We check for the first decimal value on the left side as a row value and we check for the second decimal value on the top as a column value. The intersection of this row and column corresponding to 0.3 and 0.07 gives a probability value which is 0.6443.
Hence the probability that the coin will show heads fewer than 17 times is 0.6443.

Note: To answer this question, students are required to know normal distribution and binomial approximation methods. Care must be taken while reading the question because if the value of x was taken as 17 instead of 16, we could get a completely wrong answer. We also need to be careful while reading data from the normal distribution table.