Question

(a)Explain why for a charge configuration, the equipotential surface through a point is normal to the electric field at that point ?
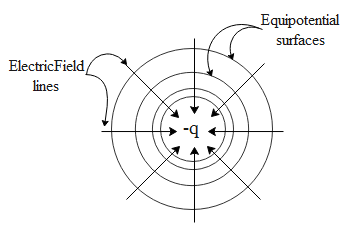
Draw a sketch of equipotential surfaces due a single charge (-q), depicting the electric field due to the charge.
(b)Obtain an expression for work done to dissociate the system of three charges placed at the vertices of an equilateral triangle of side ‘a’ as shown in the figure.

Answer 1

To obtain the answer of the first i.e. why the electric field is perpendicular to the surface is with respect to the contradiction of the definition of an equipotential surface. The electric field due to a negative charge is radially inwards, hence while sketching we need to show its direction. In the above figure we can see that the charges are arranged along the vertices of an equilateral triangle. The energy of dissociation is equal to the formation of the assembly of the charges. It is to be assumed that the charges are brought in the influence of each other from infinity.

Complete answer:
Let us first define the equipotential potential surfaces, understand the properties and the relation between electric field and electrostatic potential which results in equipotential surfaces.
An equipotential surface is a surface with a constant value of potential at all the points on the surface.
Since, to move a charge q from a region of one potential let us say A to some other potential let us say B work done is give by $\dfrac{W}{q}={{V}_{B}}-{{V}_{A}}J$.

Now since we know that on an equipotential surface, potential is the same, work done to move a charge between any two points i.e.
$\begin{aligned} & \dfrac{W}{q}={{V}_{B}}-{{V}_{A}}J \\\ & \dfrac{W}{q}=V-V \\\ & W=0J \\\ \end{aligned}$

The equipotential surfaces are always perpendicular to the direction of the field.This is because if the electric field was not perpendicular to the equipotential surface there would have existed some nonzero component along the surface. Hence to move a test charge along the direction of the field work had to be done. But this contradicts the above definition of an equipotential surface. Hence the electric field is always perpendicular to the surface.
Given below is a diagram, equipotential surfaces due a single charge (-q), depicting the electric field due to the charge.

Now let us solve question b.
Let us say we bring a charge q from infinity to A point which lies at a distance r from a charge Q. hence the work done in bringing the charge q from infinity to the point is given by,
$E=\dfrac{Qq}{4\pi {{\in }_{{}^\circ }}r}J$
Initially let us say we bring a charge q to form the above assembly as shown in the figure. The work done in doing so is zero because initially there are no other charges in the system whose potential is felt by charge q.

Further let us say we bring charge 2q and place it at a distance of a from the charge q. Hence the work done in doing so is,
$E=\dfrac{q\left( 2q \right)}{4\pi {{\in }_{{}^\circ }}a}=\dfrac{2{{q}^{2}}}{4\pi {{\in }_{{}^\circ }}a}$
Further let us say we bring charge -4q and place it at a distance of a from both the charges i.e. 2q and q. Hence the work done in doing so is,

$\begin{aligned} & E=\dfrac{q\left( -4q \right)}{4\pi {{\in }_{{}^\circ }}a}+\dfrac{2q\left( -4q \right)}{4\pi {{\in }_{{}^\circ }}a} \\\ & E=\dfrac{-4{{q}^{2}}}{4\pi {{\in }_{{}^\circ }}a}+\dfrac{-8{{q}^{2}}}{4\pi {{\in }_{{}^\circ }}a}=\dfrac{-12{{q}^{2}}}{4\pi {{\in }_{{}^\circ }}a} \\\ \end{aligned}$

The total energy in forming the above assembly is equal to,
$\begin{aligned} & E=\dfrac{2{{q}^{2}}}{4\pi {{\in }_{{}^\circ }}a}+\dfrac{-12{{q}^{2}}}{4\pi {{\in }_{{}^\circ }}a} \\\ & E=\dfrac{-10{{q}^{2}}}{4\pi {{\in }_{{}^\circ }}a}J \\\ \end{aligned}$
Since the energy of formation is equal to the energy of dessociating the system, the energy of dissociation is, $E=\dfrac{10{{q}^{2}}}{4\pi {{\in }_{{}^\circ }}a}J$

Note:
For a charge (-q) the field is not uniform $\dfrac{dV}{dr}=-\overline{E}$ is not constant for consecutive equipotential surfaces as we move from the centre of the charge but for a uniform field i.e. by a charged plate $\dfrac{dV}{dr}=-\overline{E}$ is constant. The minus sign in the formation energy of the system indicates that there is no net energy expended on the system.