Question
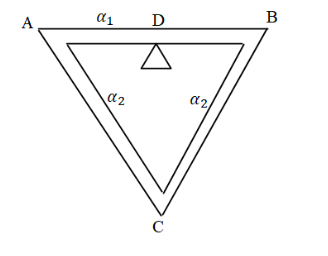
Question: A equilateral triangle ABC is formed by joining three rods of equal lengths and D is the midpoint of...
A equilateral triangle ABC is formed by joining three rods of equal lengths and D is the midpoint of AB. The coefficient of linear expansion for AB is α1andα2, if distance DC remains constant for small changes in temperature is
A) α1=α2.
B) α1=4α2.
C) α2=4α1.
D) α1=21⋅α2.
Solution
When a metal is heated then the molecules in the rod get excited and also there is expansion that takes place. When a rod is heated then there is expansion of the rod depending on the thermal coefficient and change of temperature. The formula of the thermal expansion can be used to calculate the relationship between the different rods that has been asked in the problem.
Formula used: The formula for the expansion of the rod is given by, L1=L(1+αΔT) where the change in the length isΔL,α is the coefficient of thermal expansion, ΔT is the change in temperature and L1 is the new length of the rod.
Complete step by step answer:
The length DC does not change for small changes in temperature. This is given in the problem, also it is given that the length of the three rods is equal.
Let us calculate the value of DC,
As in the triangle ADC, DC is the perpendicular, AC is hypotenuse and AD is the base.
Applying the Pythagoras theorem.
AC2=AD2+DC2 ⇒L2=(2L)2+DC2 ⇒DC2=L2−(2L)2 ⇒DC2=L2−4L2 ⇒DC=L2−4L2 ⇒DC=3⋅2L………eq.(1)
As after change in the temperature the length DC is constant and DC depends upon the lengths of AD and AC. Let us replace the value for change in temperature.
Length for DC is unchanged for change in temperature but for the change in length with change in temperature for rods AB, AC and BC.
The length of DC after change in temperature.
Since,
AC2=AD2+DC2 DC2=AC2−AD2
Put the value of DC from the equation (1). Also the change in length of the two rods is given by AC’ and AD’.
{L_1} = L\left( {1 + {\alpha _2}\Delta T} \right) \\
AC' = L\left( {1 + {\alpha _2}\Delta T} \right) \\
{L_2} = L\left( {1 + {\alpha _1}\Delta T} \right) \\
AD' = L\left( {1 + {\alpha _1}\Delta T} \right) \\
\Rightarrow \dfrac{3}{4}{L^2} = {\left( {AC'} \right)^2} - {\left( {AD'} \right)^2} \\
\Rightarrow \dfrac{3}{4}{L^2} = {\left[ {L\left( {1 + {\alpha _2}\Delta T} \right)} \right]^2} - \dfrac{1}{4}{\left[ {L\left( {1 + {\alpha _1}\Delta T} \right)} \right]^2} \\
\Rightarrow \dfrac{3}{4}{L^2} = {L^2}\left[ {1 + {{\left( {{\alpha _2}\Delta T} \right)}^2} + 2{\alpha _2}\Delta T} \right] - \dfrac{1}{4}{L^2}\left[ {1 + {{\left( {{\alpha _1}\Delta T} \right)}^2} + 2{\alpha _1}\Delta T} \right] \\
\Rightarrow \dfrac{3}{4} = \left[ {1 + {{\left( {{\alpha _2}\Delta T} \right)}^2} + 2{\alpha _2}\Delta T} \right] - \dfrac{1}{4}\left[ {1 + {{\left( {{\alpha _1}\Delta T} \right)}^2} + 2{\alpha _1}\Delta T} \right] \\
\Rightarrow \dfrac{3}{4} = \dfrac{{4\left[ {1 + {{\left( {{\alpha _2}\Delta T} \right)}^2} + 2{\alpha _2}\Delta T} \right] - \left[ {1 + {{\left( {{\alpha _1}\Delta T} \right)}^2} + 2{\alpha _1}\Delta T} \right]}}{4} \\
\Rightarrow 3 = 4\left[ {1 + {{\left( {{\alpha _2}\Delta T} \right)}^2} + 2{\alpha _2}\Delta T} \right] - \left[ {1 + {{\left( {{\alpha _1}\Delta T} \right)}^2} + 2{\alpha _1}\Delta T} \right] \\
\Rightarrow 3 = 3 + 4{\left( {{\alpha _2}\Delta T} \right)^2} + 8{\alpha _2}\Delta T - {\left( {{\alpha _1}\Delta T} \right)^2} - 2{\alpha _1}\Delta T \\
\Rightarrow 0 = 4{\left( {{\alpha _2}\Delta T} \right)^2} + 8{\alpha _2}\Delta T - {\left( {{\alpha _1}\Delta T} \right)^2} - 2{\alpha _1}\Delta T \\
\Rightarrow 0 = 4{\left( {{\alpha _2}\Delta T} \right)^2} + 8{\alpha _2}\Delta T - {\left( {{\alpha _1}\Delta T} \right)^2} - 2{\alpha _1}\Delta T \\
\Rightarrow 0 = 8{\alpha _2}\Delta T - 2{\alpha _1}\Delta T \\
\Rightarrow 8{\alpha _2}\Delta T = 2{\alpha _1}\Delta T \\
\Rightarrow 4{\alpha _2} = {\alpha _1} \\
