Question

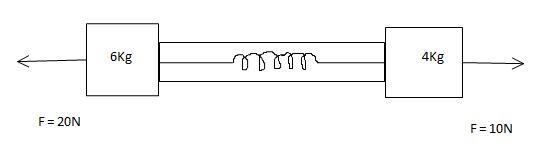
A dynamometer is attached to two blocks of masses 6Kg and 4Kg. Forces of 20N and 10N are applied on the blocks as shown in figure. Find the dynamometer reading in the steady state.

Answer 1

In the given question, we are given with two masses whose forces are given. We can find the average force by using the forces on the two masses. When we get the average force, we can assume the dynamometer reading within the calculated range. To find the dynamometer reading, we have to find the acceleration. So, the acceleration of two masses can be obtained separately and then by equating the two equations of acceleration, we can get the reading of the dynamometer.

Complete step by step solution:
According to the question, we are given:
The force on $6Kg$ mass is $20N$ .
The force on $4Kg$ mass is $10N$ .
So, we can calculate the average force on the masses.
The average force is $= \dfrac{{\left( {20 + 10} \right)}}{2} = 15N$
From the average force, the reading on the dynamometer lies between 10 and 15.
Let us assume the reading on the dynamometer to be $xN$ .
We know that force is the product of mass and the acceleration which can be written as:
Force = Mass $\times$ Acceleration
So, acceleration will be $\dfrac{{Force}}{{Mass}}$ .
Thus, we can calculate the acceleration of both the masses separately.
The acceleration of $6Kg$ mass is given by $\dfrac{{\left( {20 - x} \right)}}{6}$ .
The acceleration of $4Kg$ mass is given by $\dfrac{{\left( {x - 10} \right)}}{4}$ .
Now, equating the two equations, we get
$\dfrac{{\left( {20 - x} \right)}}{6} = \dfrac{{\left( {x - 10} \right)}}{4} \\\ 80 - 4x = 6x - 60 \\\ 140 = 10x \\\ x = \dfrac{{140}}{{10}} \\\ x = 14N \\\$
Therefore, the acceleration can be calculated by:
$a = \dfrac{{\left( {20 - 14} \right)}}{6} = 1m/{s^2}$

Therefore, the dynamometer reading will be $1m/{s^2}$.

Note: These types of questions can be solved by using basic mathematics. We should always be cautious doing such calculations because a small calculation mistake can lead us to incorrect answers. Also, we need to be precise with the details given in the question.