Solveeit Logo
Login

Question

Question: A dynamometer D is attached to two blocks of masses \(6\,kg\) and \(4\,kg\) as shown in the figure. ...

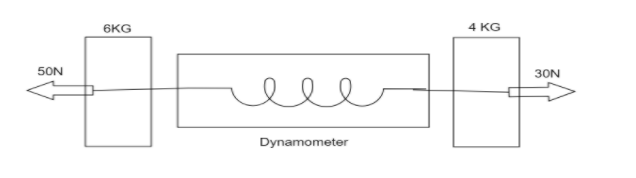
A dynamometer D is attached to two blocks of masses 6 kg6\,kg and 4 kg4\,kg as shown in the figure. The reading of the dynamometer is?

A. 18 N18\,N
B. 28 N28\,N
C. 38 N38\,N.
D. 48 N48\,N

Explanation

Solution

Hint In the question, masses of the two blocks are given. By using the equation of the newton’s second law of motion and substituting the known parameters in that equation, we get the value of the force recorded by the dynamometer.
Formula used:
F=maF = ma
Where,
FF be the force, mm be the mass and aa be the acceleration.

Complete step by step answer
Let x be the force recorded by the dynamometer
Given that the mass of the two blocks are 6 kg and 4kg6\,kg\,{\text{and }}4kg.
We know that, from the diagram both of the masses are applied in the same direction which means it is applied in one direction.
The largest force applied on the mass is 50 N50\,N and the smallest force applied on the mass is 30 N.30\,N.
So, the force is acting in the same direction. It lies between 50 and 30.
It can be written as,
30≪x≪5030 \ll x \ll 50
The resultant force on the mass, we get
6 kg mass=50−x 4 kg mass  = x−30 \begin{gathered} 6\,kg\,{\text{mass}} = 50 - x \\\ 4\,kg\,{\text{mass}}\,\, = \,x - 30 \\\ \end{gathered}
Force(F)=mass(m)×acceleration(a){\text{Force}}\left( F \right) = {\text{mass}}\left( m \right) \times {\text{acceleration}}\left( a \right)
Convert the equation of force in terms of the acceleration, we get
Acceleration(a)=Force(F)mass(m){\text{Acceleration}}\left( a \right) = \dfrac{{{\text{Force}}\left( F \right)}}{{{\text{mass}}\left( m \right)}}
Comparing the two masses and substitute the known equation in the above equation, we get
(50−x)6=(x−30)4\dfrac{{\left( {50 - x} \right)}}{6} = \dfrac{{\left( {x - 30} \right)}}{4}
Simplify the above equation, we get
200−x=6x−180200 - x = 6x - 180
x=38 N.x = 38\,N.
Therefore, the reading of the dynamometer is 38 N.38\,N.

Hence from the above options, option C is correct.

Note In the question, two masses are given. The masses are acting in the same direction. So, the force is also acting on the same plane. So, we know the expression of mass and the force. By substituting the expression in the equation of motion, we get the result.