Question

A dynamometer D is attached to two blocks of masses 6 kg and 4 k as shown in the figure. The reading of the dynamometer is?

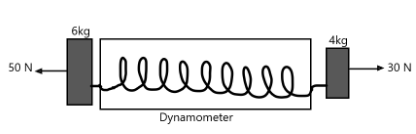
(A) 18 N
(B) 28 N
(C) 38 N
(D) 48 N

Answer 1

Hint : A dynamometer is a measuring device which can be used to measure force. The two blocks will move with the same acceleration in a particular direction.

Formula used: In this solution we will be using the following formula;
$\Rightarrow {F_{NET}} = ma$ where ${F_{NET}}$ is the resultant force, $m$ is the mass of the body, and $a$ is the acceleration of the body.

Complete step by step answer
The dynamometer is a device which can be used to measure force. For example, if a force $F$ acts on a mass connected to a dynamometer to accelerate it, the equation of the dynamometer system can be given as
$\Rightarrow F - T = ma$ where $T$ is like a resistive force due to other forces acting on the dynamometer. When such does not exist then $T = 0$ , and the dynamometer measures zero, since the dynamometer accelerates with the mass.
This is similar to a stone in free fall but attached to a string, the string will have no tension (since it will also be in free fall) and hence doesn’t “know” that it is connected to a stone.
However, when there’s a force pulling in the other direction, $T \ne 0$ . This is similar to a pulley system where another mass is hung at the other side resisting the downward acceleration of the first body.
For this spring dynamometer, the best way to measure the force will be for it to be in equilibrium.
In our question, a force of 50 N is acting on a 6 kg block attached to a dynamometer, and a force of 30 N is acting on a 4 kg block attached to the same dynamometer on the other side. The whole system must accelerate in a particular direction.
We apply Newton’s second law on each mass as in
$\Rightarrow 50 - T = 6a$ where the force experienced by the dynamometer, hence the reading on the dynamometer.
Also for 4 kg mass
$\Rightarrow T - 30 = 4a$ .
Solving simultaneously, we can multiply $50 - T = 6a$ by 2, and $T - 30 = 4a$ by 3, then subtract to eliminate $a$ , as in
$\Rightarrow 100 - 2T = 12a$
$\Rightarrow 3T - 90 = 12a$
Subtracting, we get
$\Rightarrow - 5T + 190 = 0$
Hence,
$\Rightarrow T = \dfrac{{190}}{5} = 38N$
Thus, the correct option is C.

Note
For clarity, we say that the dynamometer will able to measure the force at equilibrium because, at equilibrium $a = 0$ , hence from $F - T = ma$ we have that
$\Rightarrow F = T$ .
However, note that the force $T$ measured by the dynamometer is not inaccurate or something. Rather, instead of measuring the force on one block, like the 50 N or 30 N, it measures the force which actually allows the system to move at that particular acceleration (Like the tensional force of the string in a pulley system).