Question

A drunkard walking in a narrow lane takes 5 steps forward and 3 steps backward, followed again by 5 steps forward and 3 steps backward, and so on. Each step is 1m long and requires 1s. Plot the x-t graph of his motion. Determine graphically and otherwise how long the drunkard takes to fall in a pit 13m away from the start.

Answer 1

Calculate the total steps he moved after going 5 steps forward and 3 steps backward. Also calculate time taken by him in moving the net steps forward. In this way calculate the time taken by him to reach the pit. Do not consider backward steps if he reaches the pit during his forward steps.

Complete step-by-step answer:
Given that each step is 1m long and requires $1s$.
Therefore, for steps he moves 5m forward and 3m backward.
To move 5 steps forward he will take 5s and to move 3 steps backward he will take$3s$.
Let us consider one slot of going forward and coming back, therefore,
$1\text{ }slot=going\text{ }forward+coming\text{ }backward$
In one slot as he moves 5 steps forward and 3 steps backward, he will move a total 2 steps forward in 1 slot.
Also, the duration of a slot will be equal to $5s+3s=8s$.
After the second slot he will move 4 steps forward and will spend $16s$.
After the third slot he will move 6 steps forward and will spend $24s$.
After the fourth slot he will move 8 steps forward and will spend $32s$.
Now, he is just 5m away from the pit as the pit is 13m away from the start.
So, in the next 5 steps in the fifth slot he will fall in the pit.
As he will take 5s for 5 steps, time taken to fall in the pit will be equal to $32s+5s=37s$.
Thus, after 37s from the start, he will fall in a pit which is 13m away from the start. The following graph shows the motion of the drunkard. The distance covered by the drunkard is plotted against time taken by him to cover that distance. From the graph you can visualize his motion, going 5 steps forward and coming 3 steps backward. You can see from the graph that after $37s$ he will fall in a pit.

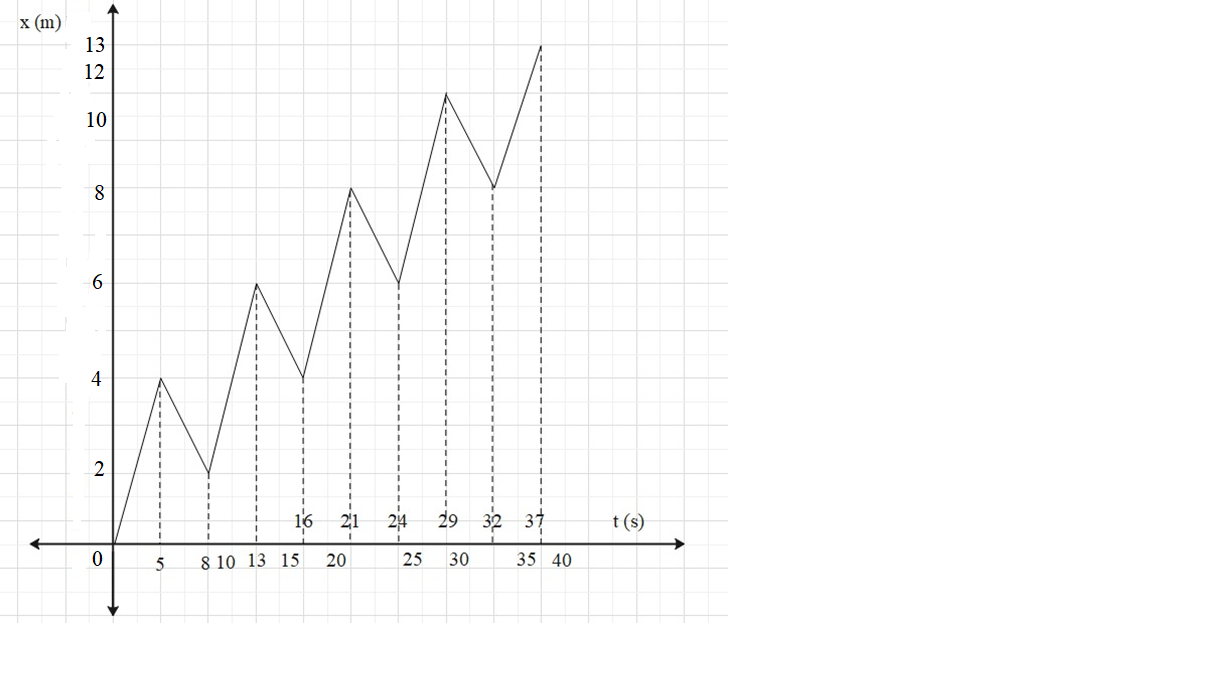
Note: Note that in this type of problem you should be careful about total steps in reaching the destination. Do not just add resultant 2m forward steps and 8s he took to take these steps. As in the fifth cycle he will have already fallen in a pit in his forward motion, you don’t have to consider the backward motion.