Question
Question: A drum placed on the floor is filled with a liquid of almost no viscosity to a height H. A small ope...
A drum placed on the floor is filled with a liquid of almost no viscosity to a height H. A small opening is made at a height h from the base. The liquid jet strikes the floor at a distance x from the wall of the drum then maximum value of x is:
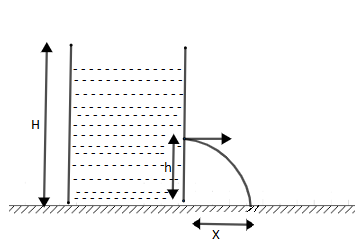
A. 21(H−h)B. HC. 21(H+h)D. x+hhH
Solution
In order to find a solution to this question we will use ton celli’s theorem, by using the formula of celli’s theorem we will find velocity and then we put this value of velocity in the equation of the motion to find the distance x.
Formula used:
v=2gh
s=ut+21at2
Complete step by step solution:
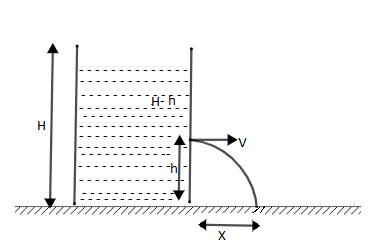
Now first we will find velocity using ton celli’s theorem which is given by
⇒v=2gh.....(1)
Where, v = velocity
g = acceleration of the gravity
h = height of the water above the hole.
Here h is height of the water above the hole which (H-h) now substitute value of h in equation (1) we get,
⇒v=2g(H−h)....(2)
Now velocity also given by,
velocity(v)=time(t)displacement(x)
Time (t) will be
t=vx....(3)
Here we can apply the equation of motion for water flowing outside in downwards direction.
s=ut+21at2
Where, s = distance
u = initial velocity
a = acceleration
t = time
Here s = h
Initial velocity will be zero and “a” will be the acceleration at gravity g, therefore our new equation will be,
h=(0)×t21gt2....(4)
Now substitute value of equation (3) in equation (4)
h=0+21g×(vx)2
Now substitute the value of v from the equation (1)
& \Rightarrow h=\dfrac{1}{2}\times g\times \dfrac{{{x}^{2}}}{{{\left( \sqrt{2g\left( H-h \right)} \right)}^{2}}} \\\ & \Rightarrow h=\dfrac{g}{2}\times \dfrac{{{x}^{2}}}{2g\left( H-h \right)} \\\ & \Rightarrow {{x}^{2}}=2\times 2.h\left( H-h \right) \\\ & \Rightarrow {{x}^{2}}=4Hh-4{{h}^{2}} \\\ & \therefore x=\sqrt{4Hh-4{{h}^{2}}}.....\left( 5 \right) \\\ \end{aligned}$$ Now to find the ${{x}_{\max }}$ we differentiate ${{x}^{2}}$ with respect to h and we will equalize with the zero. $\begin{aligned} & \Rightarrow \dfrac{d\left( x_{\max }^{2} \right)}{dh}=4H-8h=0 \\\ & \Rightarrow 8h=4H \\\ & \therefore h=\dfrac{H}{2}......\left( 6 \right) \\\ \end{aligned}$ Now we will put the value of equation (6) into equation (5) $\Rightarrow {{x}_{\max }}=\sqrt{4H\left( \dfrac{H}{2} \right)-4{{\left( \dfrac{H}{2} \right)}^{2}}}$ $\begin{aligned} & \Rightarrow {{x}_{\max }}=\sqrt{2{{H}^{2}}-{{H}^{2}}} \\\ & \Rightarrow {{x}_{\max }}=\sqrt{{{H}^{2}}} \\\ & \therefore {{x}_{\max }}=H \\\ \end{aligned}$ **Hence, option (2) H is correct.** **Note:** When we want to find the maximum distance x we have to equalize with by differentiating with respect to height h. Which is shown in the solution if we skip this step it will lead us to the wrong answer.