Question

A driving mirror consists of a cylindrical mirror of radius of curvature 10 cm and the length over the curved surface is 10 cm. If the eye of the driver be assumed to be at a great distance from the mirror, then field of view in radian is
A. 2.0
B. 4.0
C. 3.0
D. 5.0

Answer 1

To answer this question, we should be having an idea about the concept of cylindrical mirror. In the question, radius of curvature and length of curved surface of the mirror is given, we will find the focal length of the mirror from this. Radius of curvature is twice the focal length. We will assume the driver to be at infinity. Angles tend by an arc will be the field of view and it is given as the ratio of the length of the arc to the radius.

Formula used:
$\text{Angle = }\dfrac{\text{arc}}{\text{radius}}=\dfrac{l}{r}$

Complete answer:

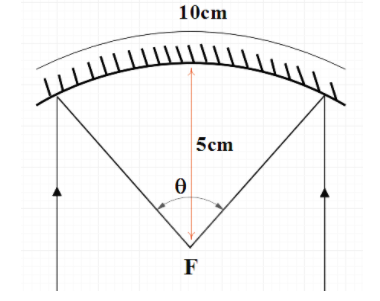
Let us assume that the driver is at infinity. So the light rays assumed to be coming from infinity. We know that if light is coming from infinity, it will be focused at the focal point.
Let the length of the curved surface be l.
Let the radius of curvature be r.
Here, the image will be focused at F. So the radius of the arc will be F.
But we know focal length is twice the radius of curvature of the mirror. That is,
$R=2f$
Then,
$f=\dfrac{R}{2}=\dfrac{10}{2}=5cm$
So, the radius of curvature for arc from image will be,
$r=5cm$
Now, to find the field of view, we must find the angle tended by the image to the arc.
So, we will take the following equation into consideration for solving the given question.
$\text{Angle = }\dfrac{\text{arc}}{\text{radius}}=\dfrac{l}{r}$
$\theta =\dfrac{l}{r}$
In this case,

l=10cm \\\ r=5cm \\\ \end{array}$$ Then, $\text{ }\\!\\!\theta\\!\\!\text{ = }\dfrac{10\text{ cm}}{5\text{ cm}}=2rad$ **Therefore, the correct option for this question is Option A.** **Note:** We know that cylindrical mirrors can produce images which are flipped upside down. But we should not confuse them with being reversed. The image that we will see through a cylindrical mirror, will depend on the orientation of the mirror. We will also have to take the distance between the mirror and the observer into consideration.