Question

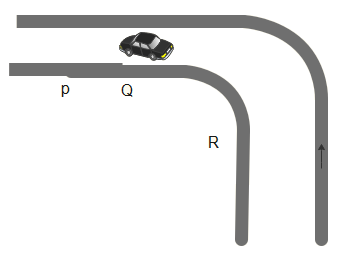
A Driver is driving his car along a road as shown in figure. The driver makes sure that the speedometer reads exactly 40 km/h. What happens to the speed of the car from P to Q?

A. Speed remains constant
B. Speed first increases then decreases
C. Speed first decreases then increases
D. Nothing can be decided.

Answer 1

As we can see in figure, path from point P to point Q is straight and it is along the road. Speedometer reads the exact value of speed which is 40 km/h. We know that magnitude of velocity is a speed. Consider so even though direction of velocity is changing but magnitude of velocity will be the same, since the speedometer reads 40 km/h throughout point P to Q.

Complete step by step answer:
A driver is driving his car along the road. While driving, the driver makes sure that the speedometer reads exactly 40km/h. Now we need to find out the speed of the car from point P to point Q. We know that the velocity of a car is nothing but the rate of change of displacement with respect to time. In simple language, velocity shows that at what time, a car does displacement. Velocity has both magnitude and direction therefore velocity is a vector quantity. If we take magnitude of velocity, we get speed. That is, the magnitude of velocity is nothing but speed.
In this case a car is covering a 40 km distance within one hour time. The car driver also makes sure that the speedometer will not deflect i.e. will not change its reading other than 40 km/h. So no matter what is the direction of the car i.e. if velocity is changing its direction but between point P and point Q direction is always constant so speed as well as velocity both are constant.

So, the correct answer is “Option A”.

Additional Information: When a car is moving along A curved road, it is performing a circular motion, since the curved road seems like an arc of a circle. Centripetal force is necessary force for circular motion. In absence of centripetal force the car would move along a tangent and circular motion is not possible.

Note: In this path along the point P and point Q is straight but the path from P to point R is curved. So we need to use the concept of banking on the road. And velocity given in this case is given as $v=\sqrt{\mu rg}$. Consider If the velocity exceeds this then $v=\sqrt{\mu rg}$, the car will be thrown off. Therefore we can say this is a safety speed or velocity with which or will turn smoothly.