Question

A double star is a system of two stars of masses m and 2m, rotating about their centre of mass only under their mutual gravitational attraction. If r is the separation between these two stars then their time period of rotation about their centre of mass will be proportional to?
A) ${r^{\dfrac{3}{2}}}$
B) $r$
C) ${m^{\dfrac{1}{2}}}$
D) ${m^{\dfrac{- 1}{2}}}$

Answer 1

First we have to keep in mind there is equilibrium force acted which is related to gravitational and centrifugal forces. As the question says distance between the stars is r, substitute their formula and consider the center of mass of the system to get x value. Through this we find angular velocity by substituting these values we get a time period of rotation.

Complete Step by step solution:

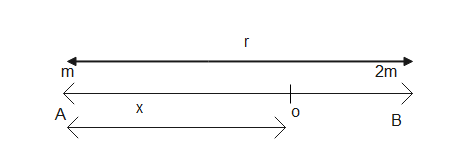
Consider equilibrium,
${F_{gravitation}} = {F_{centrifugal}} - - - - - - (1)$

In the question, the distance between the stars is r. So we can write
${F_{gravitation}} = \dfrac{{Gm(2m)}}{{{r^2}}}$
Where $m$ and $2m$ are the masses of the two stars respectively.
$r$ is the distance between two stars as shown in the figure.

For point O to be the center of mass of the system then,
3m(x) = 0+2m
$\Rightarrow x = \dfrac{{2r}}{3}$

Let the stars of mass m revolve around o with angular velocity w.
Then we have,
${F_{centrifugal}} = m\left( {\dfrac{{2r}}{3}} \right){w^2}$

Thus equation 1 become,
\eqalign{ & \Rightarrow \dfrac{{Gm(2m)}}{{{r^2}}} = m\left( {\dfrac{{2r}}{3}} \right){\omega ^2} \cr & \Rightarrow \dfrac{{G3m}}{{{r^3}}} = {\omega ^2} \cr & \Rightarrow \omega = \sqrt {\dfrac{{G3m}}{{{r^3}}}} \cr & \cr}
Where $w$ is angular velocity which, has value,
$w = \dfrac{{2\pi }}{T}$

Hence we have
\eqalign{ & \Rightarrow T = \dfrac{{2\pi }}{{\sqrt {\dfrac{{G3m}}{{{r^3}}}} }} \cr & \therefore T = \dfrac{{2\pi {r^{\dfrac{3}{2}}}}}{{{{\left( {3mG} \right)}^{\dfrac{1}{2}}}}} \cr}
Where T is period of time

Therefore, $T \propto {r^{\dfrac{3}{2}}}$. Hence, the correct options are A and D .

Additional information:
Angular velocity is nothing but it is measured in angle per unit time or radians per second It is also known as rotational velocity. The rate of change of angular velocity is angular acceleration.
Remember the angular velocity w is a vector quantity which is constant for all the particles comprising the motion, the symbol for angular velocity is omega.

Note:
In this question we have to clearly understand the question by drawing the diagram. If you have the best hold in theoretical then we can answer this question directly. Remember the period of time final equation which is used to solve the related problems.