Question

A double star consists of two stars having masses $m$ and $2m$ separated by a distance $r$. Which of the following options is correct?
A) The radius of the circular path traced by $2m$ is $\dfrac{{2r}}{3}$ .
B) The kinetic energy of the heavier star is double that of the lighter star.
C) The period of revolution of the stars is not the same.
D) The angular momentum of the lighter star is more.

Answer 1

The two stars have a mutual gravitational attraction which provides the centripetal force of rotation for each star. The two stars thus revolve about the centre of mass of the system. The distance of the star (lighter star or heavier star) from the centre of mass of the system will be the radius of the circular path described by it as it revolves.

Formulas used:
-The gravitational force of attraction between the two bodies is given by, ${F_G} = \dfrac{{GMm}}{{{r^2}}}$ where $M$ and $m$ are the masses of the heavier body and lighter body respectively, $G$ is the gravitational constant and $r$ is the distance of separation between them.
-The centripetal force acting on a mass $m$ is given by, ${F_c} = m{\omega ^2}r$ where $\omega$ is the angular velocity of the mass and $r$ is the radius of the circle described by the mass.
-The kinetic energy of a mass $m$ is given by, $K = \dfrac{1}{2}m{\left( {r\omega } \right)^2}$ where $\omega$ is the angular velocity of the mass and $r$ is the radius of the circle described by the mass.
-The angular momentum of a mass $m$is given by, $L = m{r^2}\omega$ where $r$ is the radius of the circle described by the mass and $\omega$ is the angular velocity of the mass.

Complete step by step answer.
Step 1: Sketch a figure depicting the double star system and list its parameters.

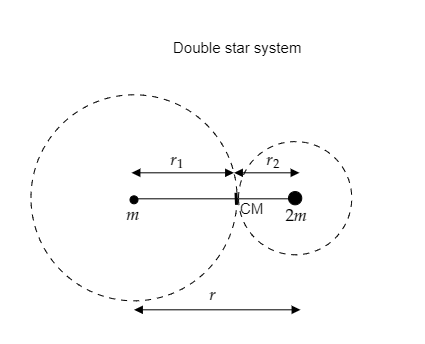
The two stars of masses $m$ and $2m$ are separated by a distance $r$ as shown in the above figure.
The centre of mass of the system lies at a distance ${r_1}$ from the lighter mass and ${r_2}$ from the heavier mass. These distances will be the radius of the circle described by the revolution of the stars.
We know from the concept of centre of mass, $m{r_1} = 2m{r_2}$ .
$\Rightarrow {r_1} = 2{r_2}$
From the figure we have $r = {r_1} + {r_2}$ .
$\Rightarrow {r_2} = r - {r_1}$
So substituting for ${r_1} = 2{r_2}$ in the above relation we get, ${r_2} = r - 2{r_2}$
$\Rightarrow {r_2} = \dfrac{r}{3}$ and ${r_1} = \dfrac{{2r}}{3}$
Thus the radius of the circular orbit of the heavier mass is $\dfrac{r}{3}$ .
So option A is incorrect.
Step 2: Express the centripetal force of each star to obtain their respective angular velocities and then their period of revolution.
Lighter star
The centripetal force of the lighter star is given by, ${F_c} = m{\omega _1}^2{r_1}$ where ${\omega _1}$ is its angular velocity and ${r_1} = \dfrac{{2r}}{3}$ is the radius of its circular orbit.
The centripetal force is equal to the gravitational force of attraction.
i.e., ${F_c} = {F_G}$
The gravitational force of attraction between the stars is given by, ${F_G} = \dfrac{{G2m \times m}}{{{r^2}}}$ where $2m$ and $m$ are the masses of the heavier star and lighter star respectively, $G$ is the gravitational constant and $r$ is the distance of separation between them.
So we have $m{\omega _1}^2\left( {\dfrac{{2r}}{3}} \right) = \dfrac{{G2m \times m}}{{{r^2}}}$
Cancelling out the similar terms and simplifying the above equation we get, ${\omega _1}^2\left( {\dfrac{r}{3}} \right) = \dfrac{{Gm}}{{{r^2}}}$
$\Rightarrow {\omega _1}^2 = \dfrac{{3Gm}}{{{r^3}}}$ or ${\omega _1} = \sqrt {\dfrac{{3Gm}}{{{r^3}}}}$
Then the period of revolution of the lighter star will be ${T_1} = \dfrac{{2\pi }}{{{\omega _1}}} = 2\pi \sqrt {\dfrac{{{r^3}}}{{3Gm}}}$
Heavier star
The centripetal force of the heavier star of mass $2m$ is given by, ${F_c} = 2m{\omega _2}^2{r_2}$ where ${\omega _2}$ is its angular velocity and ${r_2} = \dfrac{r}{3}$ is the radius of its circular orbit.
The centripetal force is equal to the gravitational force of attraction.
i.e., ${F_c} = {F_G}$
The gravitational force of attraction between the stars is given by, ${F_G} = \dfrac{{G2m \times m}}{{{r^2}}}$ where $2m$ and $m$ are the masses of the heavier star and lighter star respectively, $G$ is the gravitational constant and $r$ is the distance of separation between them.
So we have $2m{\omega _2}^2\left( {\dfrac{r}{3}} \right) = \dfrac{{G2m \times m}}{{{r^2}}}$
Cancelling out the similar terms and simplifying the above equation we get, ${\omega _2}^2\left( {\dfrac{r}{3}} \right) = \dfrac{{Gm}}{{{r^2}}}$
$\Rightarrow {\omega _2}^2 = \dfrac{{3Gm}}{{{r^3}}}$ or ${\omega _2} = \sqrt {\dfrac{{3Gm}}{{{r^3}}}}$
Thus two stars have the same angular velocity ${\omega _1} = {\omega _2} = \omega = \sqrt {\dfrac{{3Gm}}{{{r^3}}}}$
Then the period of revolution of the heavier star will be the same as that of the lighter star given by, ${T_1} = {T_2} = 2\pi \sqrt {\dfrac{{{r^3}}}{{3Gm}}}$ .
So option C is incorrect.
Step 3: Express the relation for the kinetic energies of the two stars
The kinetic energy of the lighter star of mass $m$ is given by, ${K_1} = \dfrac{1}{2}m{\left( {{r_1}\omega } \right)^2}$ ------ (1)
Substituting for ${r_1} = \dfrac{{2r}}{3}$ in equation (1) we get, ${K_1} = \dfrac{1}{2}m{\left( {\dfrac{{2r}}{3}} \right)^2} \times {\omega ^2} = \dfrac{{2m{r^2}{\omega ^2}}}{9}$
Thus the kinetic energy of the lighter star is ${K_1} = \dfrac{{2m{r^2}{\omega ^2}}}{9}$
For the heavier star, the kinetic energy will be ${K_2} = \dfrac{1}{2} \times 2m{\left( {{r_2}\omega } \right)^2}$ ------- (2)
Substituting for ${r_2} = \dfrac{r}{3}$ in equation (2) we get, ${K_2} = \dfrac{1}{2} \times 2m{\left( {\dfrac{r}{3}} \right)^2} \times {\omega ^2} = \dfrac{{m{r^2}{\omega ^2}}}{9}$
Thus the kinetic energy of the heavier star is ${K_2} = \dfrac{{m{r^2}{\omega ^2}}}{9}$
So we have ${K_1} = 2{K_2}$
So option B is incorrect.
Step 4: Express the relation for the angular momentum of the two stars.
For the lighter star, the angular momentum is ${L_1} = m{r_1}^2\omega = \dfrac{{4m{r^2}\omega }}{9}$
For the heavier star, the angular momentum is ${L_1} = m{r_2}^2\omega = \dfrac{{m{r^2}\omega }}{9}$
So we have ${L_1} > {L_2}$ .

Thus the correct option is D.

Note: The position of the centre of mass of a system consisting of two different masses will be closer to the heavier mass. This idea was used while sketching the figure of the double-star system. As the two stars rotate in their circular orbit, the centre of mass of the double-star system will remain stationary. The relation for the linear velocity $v = r\omega$ is used while expressing the centripetal force, kinetic energy and angular momentum of the stars.