Question

A double star consists of two stars having masses M and 2M. The distance between their centres is equal to r. They revolve under their mutual gravitational interaction. Then, which of the following statements are not correct?
A. Heavier star revolves in an orbit of radius r/3.
B. Kinetic energy of the heavier star is twice the kinetic energy of the other star
C. Lighter star revolves in an orbit of radius $\dfrac{{2r}}{5}$
D. All are correct

Answer 1

Hint: Any two objects revolving under the action of gravity revolves around their common centre of mass. The gravitational force is the same for both the stars.

Formula used: Universal law of Gravitation $F = \dfrac{{GMm}}{{{R^2}}}$
Centripetal force ${F_c} = \dfrac{{m{v^2}}}{R}$
Kinetic Energy, $K.E = \dfrac{1}{2}m{v^2}$.

Complete Step by step answer:

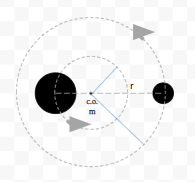
The force of gravity acting between the stars is an internal force and hence, the two-star system is under the action of no external force. This means that the center of mass of the system remains stationary and the stars revolve around this stationary center of mass.

Now, distance of centre of mass from the heavier star can be found out as:

${r_{cm}} = \dfrac{{{m_1}{r_1} + {m_2}{r_2}}}{{{m_1} + {m_2}}}$
${r_{cm}} = \dfrac{{2M \cdot 0 + M \cdot r}}{{2M + M}}$
${r_{cm}} = \dfrac{r}{3}$

So we see that the distance from the stationary center of mass to the heavier star is $\dfrac{r}{3}$. Hence statement A is correct and not our answer.

Similarly, we see that the distance of a lightyear star from the centre of mass is $r - \dfrac{r}{3}$ = $\dfrac{{2r}}{3}$. Thus the orbit of the lighter star has a radius $\dfrac{{2r}}{3}$. Statement C says that this orbit is $\dfrac{{2r}}{5}$, which is incorrect and hence, one of our answers.

Now let's see the kinetic energy relation for stars.

We know that the force experienced by the lighter star and the heavier star are the same in magnitude. We also know that this force is providing the necessary centripetal force for revolution.

So we can equate the centripetal forces of the two stars to get a relation between the speeds of two stars.

Since star A is revolving in a circle of radius $\dfrac{r}{3}$, its centripetal force can be given as $\dfrac{{{m_A}{v_A}^2}}{{{r_A}}} = \dfrac{{2M{v_A}^2}}{{\dfrac{r}{3}}}$

Similarly, for star B, the centripetal force would be $\dfrac{{{m_B}{v_B}^2}}{{{r_B}}} = \dfrac{{M{v_B}^2}}{{\dfrac{{2r}}{3}}}$

Since both of these are equal to the gravitational force of attraction, $\dfrac{{(2M){v_A}^2}}{{\dfrac{r}{3}}} = \dfrac{{M{v_B}^2}}{{\dfrac{{2r}}{3}}}$

So we see that ${v_A}^2 = \dfrac{{{v_B}^2}}{4}$.
Now the kinetic energy is $K.E = \dfrac{1}{2}m{v^2}$.

So
$K.{E_B} = \dfrac{1}{2}{m_B}{v_B}^2 = \dfrac{1}{2}M{v_B}^2$..
$K.{E_A} = \dfrac{1}{2}{m_A}{v_A}^2 = \dfrac{1}{2}(2M)\left( {\dfrac{{{v_B}^2}}{4}} \right) = \dfrac{{\dfrac{1}{2}M{v_B}^2}}{2}$.

So we see that

$K.{E_A} = \dfrac{1}{2}K.{E_B}$

Thus the Kinetic energy of a Heavier star is half that of the other. So option B is also incorrect and hence, another solution to the question.

So options B and C are wrong and hence the solutions to the problem.

Note:
1.) Do read the question properly since the question directs us to mark the incorrect options.
2.) We have assumed the orbits of stars to be circular, which is not true in general. Orbits of planets and stars are elliptical. But for most of the calculations, we assume circular orbits for planets.