Question
Question: A double convex lens is made of a glass of refractive index 1.55, with both faces of the same radius...
A double convex lens is made of a glass of refractive index 1.55, with both faces of the same radius of curvature. Find the radius of curvature required, if the focal length is 20cm.
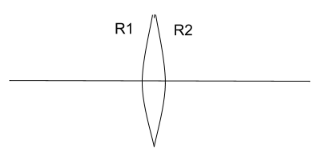
Solution
Hint: We will first consider that the radius of curvature of both the sides will be equal to the required radius of curvature in order to solve this solution further. We will also take in notice that the value of R2 will be negative as it resides on the right side of the lens.
Step By Step Answer:
Formula used: f1=(μ−1)(R11−R21)
Let the radius of curvature of the left side be R1.
Let the radius of curvature of the right side be R2.
We are asked to find out the value of R by the question.
As it is already mentioned in the question that the radius of curvature of both the sides is the same. So-
⇒R1=R2=R
We have to find out the value of R.
The value of focal length as per given in the question is 20cm.
The refractive index of the glass, as already known, is given as μ=1.55.
Now, as we know that the Lens formula in terms of μ is f1=(μ−1)(R11−R21). Applying this formula, we get-
⇒f1=(μ−1)(R11−R21) ⇒201=(1.55−1)(R11−R21)
Since we know that R1=R2=R and that R2 will be negative (right side of the lens) whereas focal length will be positive (left side of the lens)
⇒201=(1.55−1)(R1−(−R)1) ⇒201=(0.55)(R1−(−R)1) ⇒201=(0.55)(R2) ⇒201=(R1.1) ⇒R=1.1×20 ⇒R=22cm
Hence, the required radius of curvature is 22cm.
Note: Refractive index, also known as refractive ratio, measures the stretching of the light ray from one source to the next. If i is the angle of incidence of the vacuum ray (angle of the incoming ray with the perpendicular ray at the surface, called normal), and r is the angle of refraction (angle of the ray between medium and normal), the refractive index n shall be defined as the ratio of the sine to the angular sine of the refractive angle; that is to say n=sinrsini.
