Question

A diverging beam of light from a point source S having divergence angle $\alpha$, falls symmetrically on a glass slab as shown. The angles of incidence of the two extreme rays are equal. If the thickness of the glass slab is t and the refractive index n , then the divergence angle of the emergent beam is:

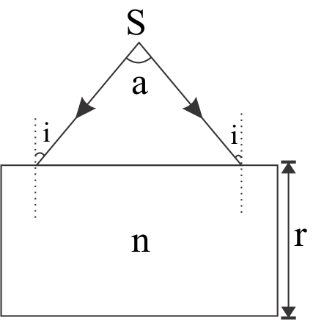
A. zero
B. $\alpha$
C. ${\sin ^{ - 1}}(1/n)$
D. $2{\sin ^{ - 1}}(1/n)$

Answer 1

Hint:- Here two divergent beam are coming and enters in the glass slab of thickness t and have refractive index of $\mu$.$\therefore$refractive index of slab is more than the air so divergent light beam will bend toward normal in the slab. then there will arise the concept of lateral shift .

Complete step-by-step solution :
As light beams are coming towards the glass slab and due to the high refractive index of the slab the light beams will bend towards the normal.
See figure for more details

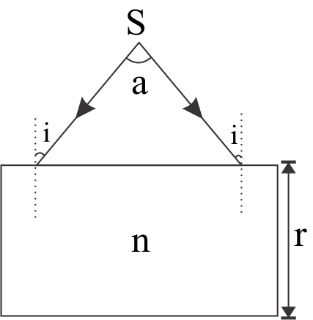
Now by seeing above figure we have concluded that
Firstly light beams are coming towards the glass slab and after entering the light beams are bending towards normal. And when again light beams are coming out from the glass slab they are again shifting as in the previous angle $\alpha$.i.e. this is the concept of lateral shift.
Hence, after shifting the angle between these diverging rays will equal to the previous angle.
So, the angle between two emergent rays will equal to $\alpha$.

Note:- When a beam of light incident parallel on an oblique medium. The light rays will shift laterally in the glass slab. The perpendicular distance between the direction of the incident rays and emergent rays is called lateral shifts.