Question

A diver at a depth of 12m in water $\left( \mu =\dfrac{4}{3} \right)$ sees the sky in a cone of semi-vertical angle of :
$\text{A}\text{. }{{\sin }^{-1}}\left( \dfrac{4}{3} \right)$
$\text{B}\text{. ta}{{\text{n}}^{-1}}\left( \dfrac{4}{3} \right)$
$\text{C}\text{. si}{{\text{n}}^{-1}}\left( \dfrac{3}{4} \right)$
$\text{D}\text{. 9}{{\text{0}}^{\circ }}$

Answer 1

When light goes from the water into air, some of the light will reflect internal. This way why the diver sees the sky in a cone. In this case, the critical angle will be equal to the semi-vertical angle of the cone. Hence, find the critical angle using Snell’s law.

Formula used:
${{\mu }_{i}}\sin i={{\mu }_{r}}\sin r$

Complete answer:
The diver under the water will not be able to see the whole sky. He can only see a circular of the sky above him. This is due to the total internal reflection of the light rays at the interface of the water at the air, when they are incident in the medium of water.
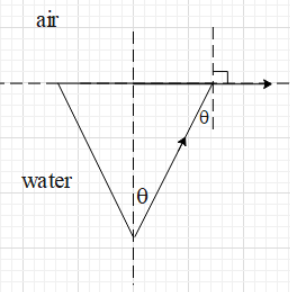
This circular section will subtend a cone on the eye of the diver (as shown in the given fig). Let the semi vertical angle of the cone $\theta$.
The light rays within this cone will pass into the medium of air. The light rays outside this cone will be completely reflected into the medium of water.
The light ray on the outermost surface of the cone will be the first ray to suffer total internal reflection. Actually, this ray will pass through the interface. Thus, it makes an angle of 90$^{\circ }$ with the normal at the interface.
As you can see in the fig, the angle of incidence for this ray is $\theta$ and the angle of refraction is 90$^{\circ }$.

Now, let us apply Snell’s law.
i.e. ${{\mu }_{i}}\sin i={{\mu }_{r}}\sin r$ ….. (i).
Here, ${{\mu }_{i}}$ is the refractive index of the medium in which the light is incident and ${{\mu }_{r}}$ is refractive index of the medium in which the light will enter after refraction. i and r are the angles of incidence and refraction respectively.
In this case, i=$\theta$, r=90$^{\circ }$, ${{\mu }_{i}}=\mu =\dfrac{4}{3}$ and ${{\mu }_{r}}$=1.
Substitute the values in equation (i).
$\Rightarrow \dfrac{4}{3}\sin \theta =1.\sin 90$ (sin 90 = 1)
$\Rightarrow \dfrac{4}{3}\sin \theta =1$
$\Rightarrow \sin \theta =\dfrac{3}{4}$
$\Rightarrow \theta ={{\sin }^{-1}}\dfrac{3}{4}$.

Hence, the correct option is C.

Note:
The angle of incidence for which the refracted light ray passes to the interface of the two mediums is called the critical angle. If the angle of incidence is greater than the critical angle, then the light ray will suffer total internal reflection.
Note that total internal reflection will happen only when the light ray is passing from a denser medium into a rarer medium.