Question

A dispatch rider is in open country at a distance of 6 kms from the nearest point P of a straight road. He wishes to proceed as quickly as possible to a point Q on the road 20 kms from P. If his maximum speed across the country is 40 kmph, 50kmph on the road, then at what distance from P, he should strike the road?

Answer 1

It is given that the dispatch rider is at least 6 km away through open country from the point P, which is on a straight road. We know that the minimum distance between a point and a line is along a perpendicular from the point to the line. Thus, we will draw the figure of the road and will assume a variable for the distance of a point from P at which the rider should enter the road so that he reaches point Q in the minimum time, when the speed of rider on road and in open country is given. The distance between point P and Q is also given to us. With the help of the figure and the information given to us, we will try to find an equation for the required time. Once we have the equation, we will find the value for which the time required is minimum. We know that to find the value of a variable at minima or maxima or both, we need to differentiate the equation once and equate it to zero. This will give us the variable and hence the distance.

Complete step by step answer:
It is given to us that the despatch rider is at least 6 km away through open country from the point P, which is on straight road. The distance PQ is 20 km. Let X be the point on the road, which is a distance x from point P, such that if the rider enters the road at point X, the time take to reach Q from the starting position will be minimum. The road map will look as follows:

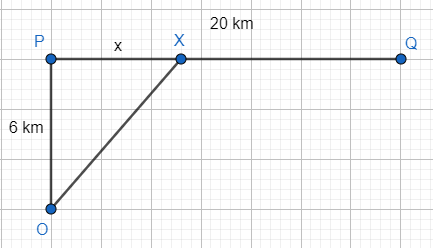
Therefore, the path taken by the rider shall be OX – XQ.
From the figure, we can see that OPX is a right-angled triangle.
Thus, $OX=\sqrt{36+{{x}^{2}}}$, by application of Pythagoras theorem.
The distance XP will be (20 – x).
We are given that the speed of the rider in country (OX) is 40 kmph and the speed on the road (XQ) is 50 kmph.
Therefore, time required to cover OX will be given as a quotient of distance OX and speed across OX.
$\Rightarrow {{t}_{OX}}=\dfrac{\sqrt{36+{{x}^{2}}}}{40}$ .
Applying the same principle, the time required to cover XQ will be ${{t}_{XQ}}=\dfrac{\left( 20-x \right)}{50}$.
Therefore, total time required to reach from O to Q will be $t\left( x \right)=\dfrac{\sqrt{36+{{x}^{2}}}}{40}+\dfrac{\left( 20-x \right)}{50}$.
Now, we need to find the value of x for which the time $t\left( x \right)$ is minimum.
We know that to find the value of a variable at minima, we need to differentiate the equation once and equate it to zero.
For differentiation we will use the chain rule, given as $\dfrac{d\left( f\left( g\left( x \right) \right) \right)}{dx}=f'\left( g\left( x \right) \right)\times g'\left( x \right)$.
We know that $\dfrac{d\sqrt{x}}{dx}=\dfrac{1}{2\sqrt{x}}$ and $\dfrac{d\left( {{x}^{2}} \right)}{dx}=2x$.
$\begin{aligned} & \Rightarrow t'=\dfrac{1}{40}\dfrac{d\left( \sqrt{36+{{x}^{2}}} \right)}{dx}+\dfrac{1}{50}\dfrac{d\left( 20-x \right)}{dx} \\\ & \Rightarrow t'=\dfrac{1}{40}\left( \dfrac{2x}{2\sqrt{36+{{x}^{2}}}} \right)+\dfrac{1}{50}\left( 0-1 \right) \\\ & \Rightarrow t'=\dfrac{1}{40}\left( \dfrac{x}{\sqrt{36+{{x}^{2}}}} \right)-\dfrac{1}{50} \\\ & \Rightarrow \dfrac{1}{40}\left( \dfrac{x}{\sqrt{36+{{x}^{2}}}} \right)-\dfrac{1}{50}=0 \\\ \end{aligned}$
Now, we will solve this equation for the value of x.
$\begin{aligned} & \Rightarrow \dfrac{x}{\sqrt{36+{{x}^{2}}}}=\dfrac{40}{50} \\\ & \Rightarrow \dfrac{{{x}^{2}}}{36+{{x}^{2}}}=\dfrac{16}{25} \\\ & \Rightarrow 25{{x}^{2}}=16\times 36+16{{x}^{2}} \\\ & \Rightarrow 9{{x}^{2}}=16\times 36 \\\ & \Rightarrow {{x}^{2}}=16\times 4 \\\ & \Rightarrow x=\pm 8 \\\ \end{aligned}$
But distance cannot be negative, hence x = 8.
To determine whether the function is maximum or minimum at the variable, we need to double derivate the function.
To perform the derivation, we need to use the chain-rule as well as product rule. The product rule is given as $\dfrac{d\left( uv \right)}{dx}=u'v+v'u$.
For our function, $u=x$ and $v=\dfrac{1}{\sqrt{36+{{x}^{2}}}}={{\left( 36+{{x}^{2}} \right)}^{-\dfrac{1}{2}}}$.

& t''=\dfrac{1}{40}\dfrac{d\left( \dfrac{x}{\sqrt{36+{{x}^{2}}}} \right)}{dx}-\dfrac{d\dfrac{1}{50}}{dx} \\\ & =\dfrac{1}{40}\left( \dfrac{1}{\sqrt{36+{{x}^{2}}}} \right)+\dfrac{1}{40}\left( x \right)\left( -\dfrac{1}{2} \right){{\left( 36+{{x}^{2}} \right)}^{-\dfrac{1}{2}-1}}\left( 2x \right)-0 \\\ & =\dfrac{1}{40}\left[ \dfrac{1}{\sqrt{36+{{x}^{2}}}}-\dfrac{x}{\left( 36+{{x}^{2}} \right)\sqrt{36+{{x}^{2}}}} \right] \end{aligned}$$ Substitute x = 8. If t’’ is greater than 0, the function is minimum at x = 8 and if t’’ is less than 0, the function is maximum at x = 8. $$\begin{aligned} & t''{{|}_{x=8}}=\dfrac{1}{40}\left[ \dfrac{1}{\sqrt{36+{{\left( 8 \right)}^{2}}}}-\dfrac{8}{\left( 36+{{\left( 8 \right)}^{2}} \right)\sqrt{36+{{\left( 8 \right)}^{2}}}} \right] \\\ & =\dfrac{1}{40}\left[ \dfrac{1}{\sqrt{36+64}}-\dfrac{8}{\left( 36+64 \right)\sqrt{36+64}} \right] \\\ & =\dfrac{1}{40\left( \sqrt{100} \right)}\left[ 1-\dfrac{8}{100} \right] \\\ & =\dfrac{1}{40\left( 10 \right)}\left[ \dfrac{92}{100} \right] \\\ & > 0 \end{aligned}$$ Since t’’ is greater than zero, the minimum of t(x) lies at x = 8. **Therefore, the rider should enter the road at a point 8 km away from point P, so that he requires minimum time.** **Note:** The other way to find a minimum is to draw a graph of the equation. But the equation with us is $t\left( x \right)=\dfrac{\sqrt{36+{{x}^{2}}}}{40}+\dfrac{\left( 20-x \right)}{50}$, which is a very complicated function and very difficult to graph on paper. Graphing utility can be used to find the minimum digitally.