Question

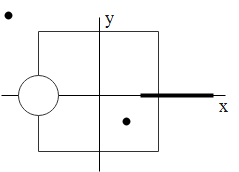
A disk of radius a/4 having a uniformly distributed charge 6C is placed in the x-y plane with centre at,(-a/2, 0, 0). A rod of length ‘a’ carrying a uniformly distributed charge 8C is placed on the x-axis from x= a/4 to x=5a/4. Two point charges -7C and 3C are placed at (a/4, -a/4, 0) and (-3a/4, 3a/4, 0), respectively. Consider a cubical surface formed by six surfaces $x=\pm a/2\text{, }y=\pm a/2\text{, }z=\pm a/2$. The electric flux through this cubical surface is:

$\begin{aligned} & a)\dfrac{-2C}{{{\in }_{0}}} \\\ & b)\dfrac{2C}{{{\in }_{0}}} \\\ & c)\dfrac{10C}{{{\in }_{0}}} \\\ & d)\dfrac{12C}{{{\in }_{0}}} \\\ \end{aligned}$

Answer 1

In the above question it is given to us that the cubical shape is placed at the centre i.e. at the origin. There exist some charge distributions which are placed at different points in the cube. Hence we will first calculate how much charge is enclosed within the cubical surface and then using gauss law we will determine the flux through the cubical surface.

Formula used:
$\phi =\dfrac{Q}{{{\in }_{0}}}$

Complete answer:
To begin with let us first see how much charge is enclosed within the cubical surface. In the question it is given to us that the disc is placed with its center at (-a/2, 0, 0). Hence we can say that half of the discs are enclosed within the cube. The charge on the disc is 6C. Further the charge is uniformly distributed on the disc. Therefore we can imply that the charge on the disc enclosed within the cube is 6C/2= 3C.

It is also given to us that the rod is placed with its two ends at a/4 to x=5a/4. Hence we can say that the length of the rod is ’a’ with total charge 8C. The surface of the cube lies at a distance of a/2. Therefore the section of the rod enclosed within the cube is a/2-a/4=a/4. The total charge on the rod of length a is given to be as 8C.Therefore the total charge of the rod enclosed within the cubical surface is 2C. It is to be noted that the charge 3C lies outside the cubical surface. It is also given that the charge -7C lies within the cubical surface i.e. at (a/4, -a/4, 0).
From the above information, the total charge (Q)enclosed within the surface is,
$\begin{aligned} & Q=3C+2C+-7C \\\ & Q=-2C \\\ \end{aligned}$
As per gauss law the total flux ($\phi$ )through a closed surface with the permittivity of free space as ${{\in }_{0}}$ is given by,
$\begin{aligned} & \phi =\dfrac{Q}{{{\in }_{0}}} \\\ & \Rightarrow \dfrac{-2C}{{{\in }_{0}}} \\\ \end{aligned}$
Therefore the total flux through the closed surface is $\dfrac{-2C}{{{\in }_{0}}}$

Note:
Usually if the total flux through the cubical surface is given as $\phi$, then we say that the total flux through each of the cubical surfaces is $\dfrac{\phi }{6}$. But in the above case this result does not hold true. This is because the charges enclosed are not solely due to test charges. The flux is due to some charge distribution. If we consider the charged disc, it will have its field only in the direction of the XY plane and not in any other plane. hence the total flux across each of the surfaces cannot be said to be equal to $\dfrac{\phi }{6}$.