Question

A disk of radius 4R & charge density (+ $\sigma$ C/m²) and a ring carrying charge Q are placed parallel at distance of R such that their central axis are same. There is point P as shown on line C₁C₂P such that potential at P is zero (C₁ & C₂ are centers of ring and disk). Then charge Q is

Answer 1

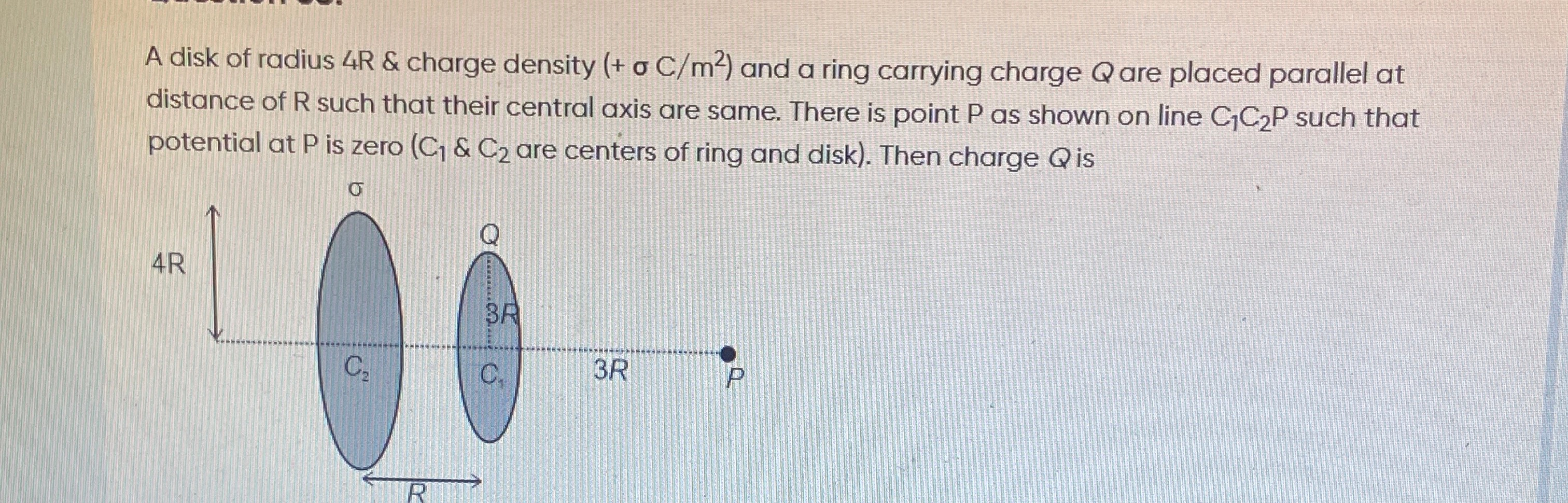
-24π σ R² (2-√2)

Answer 2

The electric potential at point P is the sum of the potentials due to the charged disk and the charged ring.

The disk has radius $R_{disk} = 4R$ and uniform surface charge density $+\sigma$. The point P is on the axis of the disk at a distance $x_{disk}$ from its center $C_2$. From the figure, the distance between the centers $C_2$ and $C_1$ is $R$, and the distance between $C_1$ and P is $3R$. Since P is on the line $C_1C_2P$ and the figure shows the order $C_2, C_1, P$, the distance from $C_2$ to P is $x_{disk} = C_2P = C_2C_1 + C_1P = R + 3R = 4R$. The potential at P due to the disk is given by:

$V_{disk}(P) = \frac{\sigma}{2\epsilon_0} (\sqrt{x_{disk}^2 + R_{disk}^2} - x_{disk})$

$V_{disk}(P) = \frac{\sigma}{2\epsilon_0} (\sqrt{(4R)^2 + (4R)^2} - 4R)$

$V_{disk}(P) = \frac{\sigma}{2\epsilon_0} (\sqrt{16R^2 + 16R^2} - 4R)$

$V_{disk}(P) = \frac{\sigma}{2\epsilon_0} (\sqrt{32R^2} - 4R)$

$V_{disk}(P) = \frac{\sigma}{2\epsilon_0} (4\sqrt{2}R - 4R)$

$V_{disk}(P) = \frac{2\sigma R}{\epsilon_0} (\sqrt{2} - 1)$

The ring has radius $R_{ring} = 3R$ and total charge $Q$. The point P is on the axis of the ring at a distance $x_{ring}$ from its center $C_1$. From the figure, the distance from $C_1$ to P is $x_{ring} = C_1P = 3R$. The potential at P due to the ring is given by:

$V_{ring}(P) = \frac{1}{4\pi\epsilon_0} \frac{Q}{\sqrt{x_{ring}^2 + R_{ring}^2}}$

$V_{ring}(P) = \frac{1}{4\pi\epsilon_0} \frac{Q}{\sqrt{(3R)^2 + (3R)^2}}$

$V_{ring}(P) = \frac{1}{4\pi\epsilon_0} \frac{Q}{\sqrt{9R^2 + 9R^2}}$

$V_{ring}(P) = \frac{1}{4\pi\epsilon_0} \frac{Q}{\sqrt{18R^2}}$

$V_{ring}(P) = \frac{1}{4\pi\epsilon_0} \frac{Q}{3\sqrt{2}R}$

The total potential at point P is the sum of the potentials due to the disk and the ring:

$V_{total}(P) = V_{disk}(P) + V_{ring}(P)$

We are given that the potential at P is zero, so $V_{total}(P) = 0$.

$\frac{2\sigma R}{\epsilon_0} (\sqrt{2} - 1) + \frac{Q}{4\pi\epsilon_0 \cdot 3\sqrt{2}R} = 0$

Now, we solve for $Q$:

$\frac{Q}{12\pi\epsilon_0 \sqrt{2}R} = - \frac{2\sigma R}{\epsilon_0} (\sqrt{2} - 1)$

Multiply both sides by $12\pi\epsilon_0 \sqrt{2}R$:

$Q = - \frac{2\sigma R}{\epsilon_0} (\sqrt{2} - 1) \cdot 12\pi\epsilon_0 \sqrt{2}R$

$Q = - 2\sigma R (\sqrt{2} - 1) \cdot 12\pi \sqrt{2}R$

$Q = - 24\pi \sigma R^2 \sqrt{2} (\sqrt{2} - 1)$

$Q = - 24\pi \sigma R^2 (\sqrt{2} \cdot \sqrt{2} - \sqrt{2} \cdot 1)$

$Q = - 24\pi \sigma R^2 (2 - \sqrt{2})$