Question

A disc rotates about its axis of symmetry in a horizontal plane at a steady rate of $3.5$revolutions per second. A coin placed at a distance of $1.25cm$ from the axis of rotation remains at rest on the disc. The coefficient of friction between the coin and the disc is then $\left( {g = 100m/{s^2}} \right)$?

Answer 1

In this question, we need to determine the coefficient of friction between the coin and the disc such that the disc rotates about its axis of symmetry in a horizontal plane at a steady rate of $3.5$revolutions per second. For this we will use the relation between the force, radius of the coin and the angular velocity of the coin which is given as $f = mr{\omega ^2}$.

Complete step by step answer:
Let us consider the disc which is rotating about an axis passing through O and perpendicular to the plane. The disc is rotating in the horizontal plane at a steady rate of $\omega = 3.5\,\,revolution/\operatorname{second}$.

We know the one revolution makes $2\pi$the radian angle. So, the value of $\omega$ in radian per second is given as,
$\Rightarrow \omega = 3.5 \times 2\pi$ $radian/\operatorname{second}$
or
$\Rightarrow \omega = 7\pi$ $radian/\operatorname{second}$
Let the coin be placed at a distance of $r = 1.25cm$ from the centre of the disc of mass m.
Since the disc is in a rotating frame, there will be a centrifugal force in the coin in a radially outward direction. As the slipping tendency of the coin is pushing the coin radially in an outward direction due to centrifugal force$\left( {mr{\omega ^2}} \right)$, the friction between the disc and coin opposes this slipping tendency of the coin.

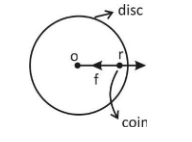
Therefore, at equilibrium, the coin remains at rest on the disc where frictional force becomes equal to centrifugal force.
$\Rightarrow f = mr{\omega ^2}$
$\Rightarrow \mu N = mr{\omega ^2}$ [N is normal and equal to mg]
$\Rightarrow \mu \left( {mg} \right) = mr{\omega ^2} \\\ \Rightarrow \mu g = r{\omega ^2} \\\ \Rightarrow \mu = \dfrac{{r{\omega ^2}}}{g} \\\ \Rightarrow \mu = \dfrac{{{{\left( {7\pi } \right)}^2} \times \left( {1.25} \right) \times {{10}^{ - 2}}}}{{10}} \\\ \Rightarrow \mu = 0.6 \\\$

Note: When a particle describes circular motion or the particle is in a rotating frame, then the particle feels centrifugal force away from the center of the rotating frame. To avoid the slipping of the particle, there must be a centrifugal force which is balanced by frictional force. To avoid the slipping of the particle, the linear acceleration must be equal to friction coefficient $\left( \mu \right)$ times gravity (g).