Question

A disc of radius $R$ rolls without slipping on a horizontal surface with velocity $v_0$ as shown in figure. Match the entries of List-I with those of List-II. [FIGURE]

List-I: (P) Acceleration of point is zero (Q) Acceleration of point is $\frac{v_0^2}{R}$ (R) Radius of curvature of the path of point is $2\sqrt{2}R$ at given instant (S) Radius of curvature of the path of point is $4R$ at given instant

List-II: (1) Point A (2) Point B (3) Point C (4) Point D (5) Point O

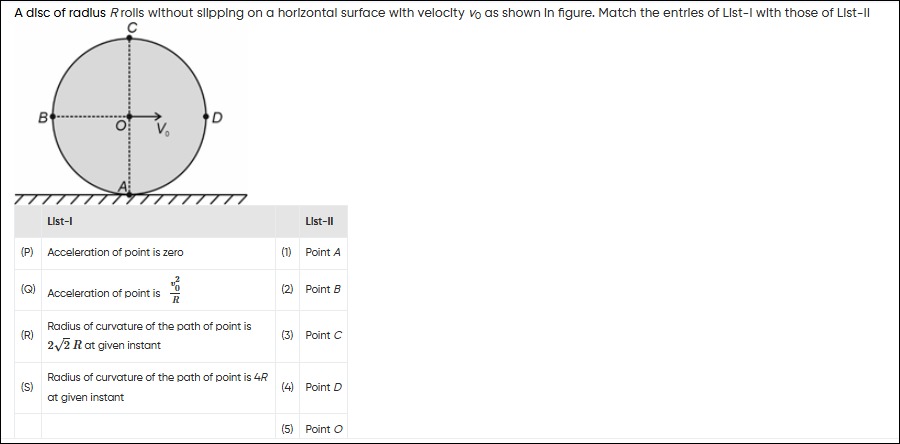
• A. (P)-(5), (Q)-(1), (2), (3), (4), (R)-(2), (4), (S)-(3)
• B. (P)-(5), (Q)-(1), (R)-(2), (S)-(3)
• C. (P)-(1), (Q)-(5), (R)-(2), (S)-(3)
• D. (P)-(5), (Q)-(1), (2), (3), (4), (R)-(2), (S)-(3)

Answer 1

Answer: (A)

(P)-(5), (Q)-(1), (2), (3), (4), (R)-(2), (4), (S)-(3)

Answer 2

For a disc rolling without slipping, the velocity of the center $v_c = v_0$ and angular velocity $\omega = v_0/R$. Assuming constant $v_0$, angular acceleration $\alpha = 0$.

Velocities:

• Point O (center): $v_O = v_0$ (horizontal)
• Point A (bottom): $v_A = 0$
• Point B (left): $v_B = \sqrt{v_0^2 + (-v_0)^2} = \sqrt{2}v_0$
• Point C (top): $v_C = v_0 + \omega R = v_0 + v_0 = 2v_0$ (horizontal)
• Point D (right): $v_D = \sqrt{v_0^2 + v_0^2} = \sqrt{2}v_0$

Accelerations: The acceleration of any point P on the rim relative to the center is centripetal: $a_{P/O} = \omega^2 R = (v_0/R)^2 R = v_0^2/R$. The acceleration of the center is zero.

• Point O: $a_O = 0$ (constant velocity)
• Point A: $a_A = a_{A/O}$ (upwards) $= v_0^2/R$
• Point B: $a_B = a_{B/O}$ (rightwards) $= v_0^2/R$
• Point C: $a_C = a_{C/O}$ (downwards) $= v_0^2/R$
• Point D: $a_D = a_{D/O}$ (leftwards) $= v_0^2/R$

Radius of Curvature of Cycloid: The path of a point on the rim is a cycloid. The radius of curvature $\rho$ is given by $\rho = 4R \sin(\theta/2)$, where $\theta$ is the angle of rotation from the lowest point.

• Point A (lowest): $\theta = 0 \implies \rho = 4R \sin(0) = 0$.
• Point D (rightmost): $\theta = \pi/2 \implies \rho = 4R \sin(\pi/4) = 4R(1/\sqrt{2}) = 2\sqrt{2}R$.
• Point C (topmost): $\theta = \pi \implies \rho = 4R \sin(\pi/2) = 4R$.
• Point B (leftmost): $\theta = 3\pi/2 \implies \rho = 4R \sin(3\pi/4) = 4R(1/\sqrt{2}) = 2\sqrt{2}R$.

Matching: (P) Acceleration of point is zero: Point O (5). (Q) Acceleration of point is $\frac{v_0^2}{R}$: Points A (1), B (2), C (3), D (4). (R) Radius of curvature is $2\sqrt{2}R$: Points B (2), D (4). (S) Radius of curvature is $4R$: Point C (3).