Question

A disc of radius R is spun to an angular speed ${\omega _0}$​ about its axis and then imparted a horizontal velocity of magnitude $\dfrac{{{\omega _{0}}R}}{4}$ ​ The coefficient of friction is $\mu$. The sense of rotation and direction of linear velocity are shown in the figure. The disc will return to its initial position

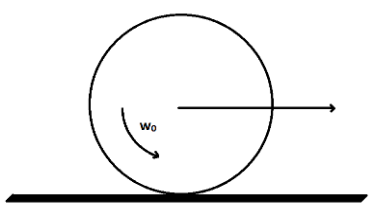
A. If the value of $\mu < 0.5$.
B. Irrespective of the value of $\mu$.
C. If the value of $0.5 < \mu < 1$.
D. If $\mu > 1$.

Answer 1

Here, we are asked to determine the value of coefficient of friction $\mu$for which the disc will return to its initial position. We know that only the bottom point of the disc is in the direct contact with the surface. Therefore, we will find the angular momentum at the most bottom point of the disc and by the help of this, we will reach our final answer.

Complete step by step answer:
Let $m$ be the mass of the disc and ${v_0}$ be the linear velocity of the disc.The angular momentum at the most bottom point can be given as:
$L = {I_C}{\omega _0} - m{v_0}R$
Where, ${I_C}$ is the moment of inertia of the disc about its center which is given by $\dfrac{1}{2}m{R^2}$.
Also, we are given that ${v_0} = \dfrac{{{\omega _{0}}R}}{4}$.
Therefore, putting these values, the angular momentum of the disc is given by:

\Rightarrow L = \dfrac{1}{2}m{R^2}{\omega _0} - \dfrac{1}{4}m{R^2}{\omega _0} \\\ \therefore L = \dfrac{1}{4}m{R^2}{\omega _0} \\\ $$ Thus, the angular momentum of the disc is positive or we can say that it is in anticlockwise direction. We can say that during slip, the friction acts about the bottommost point.Therefore, its torque is zero. In other words, the direction of angular momentum remains anticlockwise in the case of pure rolling. Therefore, it can be concluded that the disc will return to its initial position irrespective of the value of $$\mu $$. **Hence, option B is correct.** **Note:** In this question, we have concluded that the disc will return to its initial position irrespective to the value of $$\mu $$.This means that the return of the disc to its original position does not depend on the type of the surface. We will get the same result whether the surface is smooth or rough.