Question

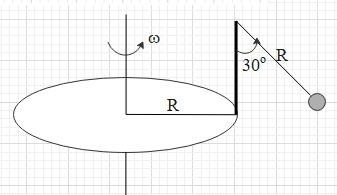
A disc of radius R has a light pole fixed perpendicular which in turn has a pendulum of length R attached to its other end as shown in the figure. The disc rotated with a constant angular velocity $\omega$. The string is making an angle ${{30}^{\circ }}$ with rod. The angular velocity $\omega$ of the disc is:

$\text{A}\text{. }{{\left( \dfrac{\sqrt{3}g}{R} \right)}^{1/2}}$
$\text{B}\text{. }{{\left( \dfrac{\sqrt{3}g}{2R} \right)}^{1/2}}$
$\text{C}\text{. }{{\left( \dfrac{g}{\sqrt{3}R} \right)}^{1/2}}$
$\text{D}\text{. }{{\left( \dfrac{2g}{3\sqrt{3}R} \right)}^{1/2}}$

Answer 1

The pendulum will rotate in a horizontal plane parallel to the plane of the disc with angular velocity $\omega$. Then find the radius of the circular path of the pendulum. Find the forces acting on the pendulum. Equate the net force in the vertical direction to zero. The pendulum will have the centripetal acceleration due to the horizontal component of the tension. They use the formula for the centripetal acceleration. Then with the equations find the value of $\omega$.
Formula used:
F = mg
F = ma
$a={{\omega }^{2}}r$

Complete answer:
When the disc is rotated with a constant angular velocity $\omega$, the attached pole will also rotate with the disc with the same angular velocity. Since the pendulum is attached to one end of the pole, the bob of the pendulum will also rotate along with the disc with the angular velocity. However, the radius of the circular path taken by the pendulum will be greater than the radius of the disc.
From the figure, we get that the radius of the circular path is $r=R+R\sin {{30}^{\circ }}=R+\dfrac{R}{2}=\dfrac{3R}{2}$.
Let's analyse the forces acting on the pendulum.
There are two forces acting on the pendulum and they are the gravitational force acting downwards and the tension of the string in the direction along the length of the string and away from the bob.

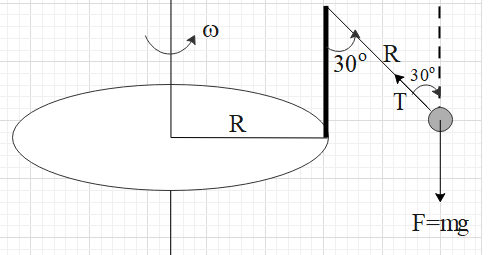
The gravitational force acting on a body of mass m is given as F = mg, where g is acceleration due to gravity.
Resolve the tension force in the horizontal and vertical components. The horizontal component will be $T\sin {{30}^{\circ }}=\dfrac{T}{2}$ and the vertical component will be $T\cos {{30}^{\circ }}=\dfrac{\sqrt{3}T}{2}$.
We know that the pendulum is rotating in the horizontal plane. Therefore, the net force in the vertical direction is zero. This means that $F=\dfrac{\sqrt{3}T}{2}$
$\Rightarrow mg=\dfrac{\sqrt{3}T}{2}$
$\Rightarrow T=\dfrac{2mg}{\sqrt{3}}$ ….. (i).
Due to the horizontal component of the tension, the pendulum undergoes rotation. And from Newton’s second law of motion we know that F=ma.
Therefore, $\dfrac{T}{2}=ma$
Substitute the value of T from equation (i)
$\Rightarrow \dfrac{\dfrac{2mg}{\sqrt{3}}}{2}=ma$
$\Rightarrow a=\dfrac{g}{\sqrt{3}}$ ….. (ii).
Here, a is the centripetal acceleration of the pendulum.
When a particle is in a rotational motion with an angular velocity $\omega$., its centripetal acceleration is given as $a={{\omega }^{2}}r$, where r is the radius of rotation.
Substitute the value of ‘a’ in equation (ii).
$\Rightarrow {{\omega }^{2}}r=\dfrac{g}{\sqrt{3}}$
Substitute the value of r.
$\Rightarrow {{\omega }^{2}}\left( \dfrac{3R}{2} \right)=\dfrac{g}{\sqrt{3}}$
$\Rightarrow {{\omega }^{2}}=\dfrac{2g}{3\sqrt{3}R}$
$\Rightarrow \omega ={{\left( \dfrac{2g}{3\sqrt{3}R} \right)}^{1/2}}$

So, the correct answer is “Option D”.

Note:
In the solution, we found the value of angular velocity in the frame of the stationary observer. We can also calculate the angular velocity by taking the frame of the pendulum as the reference. The pendulum will experience a pseudo force which is equal to ma which balances the horizontal component of the tension because the acceleration of the pendulum with respect to itself is zero.