Question

A disc of radius 0.1 m rolls without sliding on a horizontal surface with a velocity of 6 m/s. Then, it ascends a smooth continuous track as shown in the figure. Given, g= $10m/{{s}^{2}}$ , the height up to which it will ascend is (g= $10m/{{s}^{2}}$ )

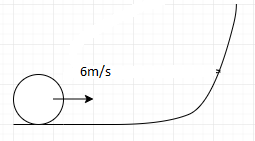
A: 2.4m
B: 0.9m
C: 2.7m
D: 1.8m

Answer 1

Hint : Here, we are given the rolling motion of a disc on a horizontal ground. In this scenario we can say that the body possesses both linear momentum as well as angular momentum. During the calculation of the kinetic energy of the motion, both these momentums should be considered during the calculation process.

Complete Step By Step Answer:
We are given that a disc of radius 0.1 m rolls without sliding on a horizontal surface with a velocity of 6 m/s. Further, it begins to ascend a smooth continuous track as pet the figure given to us.
We have to find the height up to which it will ascend.
In this case, there is only rolling motion and no sliding motion. Hence we can say that there is an absence of the influence of friction.
When the disc rolls without sliding motion, the kinetic energy of the disc can be found by
KE=\dfrac{1}{2}m{{v}^{2}}+\dfrac{1}{2}I{{\omega }^{2}}=\dfrac{1}{2}m{{v}^{2}}+\dfrac{1}{2}(\dfrac{1}{2}m{{r}^{2}})(\dfrac{{{v}^{2}}}{{{r}^{2}}})[\because v=rw] \\\ \Rightarrow KE=\dfrac{1}{2}m{{v}^{2}}+\dfrac{1}{4}m{{v}^{2}}=\dfrac{3}{4}m{{v}^{2}} \\\
At the maximum height, this transforms to potential energy. Thus we can write it as
mgh=\dfrac{3}{4}m{{v}^{2}} \\\ \Rightarrow h=\dfrac{3{{v}^{2}}}{4g} \\\
We are given that v=6m/s and g= $10m/{{s}^{2}}$
Thus, height is given by $h=\dfrac{3{{(6)}^{2}}}{4(10)}=2.7m$
Hence, option C is the correct answer among the given options.

Note :
When such questions involve acceleration we have to note the point that in such cases, both linear and tangential acceleration occurs and both should be considered during the calculation process. The situation would have been different if there was a sliding motion top of the ball. Also, we have assumed that there is no frictional force present. This problem can also be done using the work energy theorem.