Question
Question: A disc of mass \({\text{m}}\) and radius \({\text{R}}\) is attached to a rectangular plate of same m...
A disc of mass m and radius R is attached to a rectangular plate of same mass, breadth R and length 2R as shown in the figure. Find the moment of inertia of this system about the axis XX’ passing through the centre of the disc and along the plane.
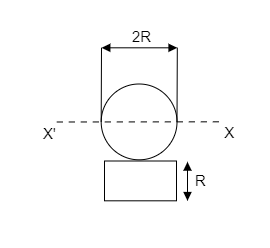
Solution
The moment of inertia of the system about the given axis will be the sum of the moment of inertia of the disc and that of the plate about the same axis. The moment of inertia of the disc about its diameter is a known quantity. The parallel axis theorem gives the moment of inertia of the plate about the given axis as the sum of the moment of inertia of the plate about its length and the product of the mass of the plate and the square of the distance between the given axis and its length.
Formulas used:
-The moment of inertia of a body about any axis as per the parallel axes theorem is given by, I′=I+Ma2 where I is the moment of inertia of the body about the parallel axis passing through its centre of mass, M is the mass of the body and a is the distance between the two parallel axes.
-The moment of inertia of a body is given by, I=Mk2 where M is the mass of the body and k is the radius of gyration.
Complete step by step answer.
Step 1: Sketch a figure depicting the two parallel axes under consideration and list the parameters involved.
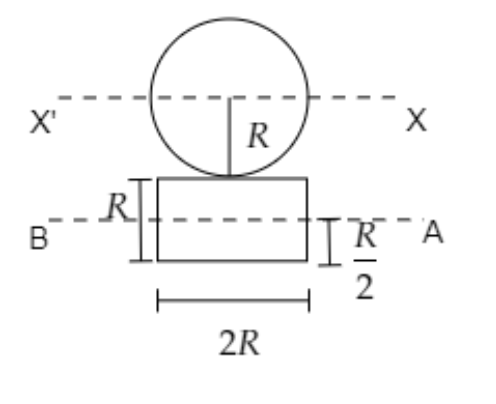
In the above figure, the axis AB taken about the length of the plate is parallel to the axis XX’.
The mass of the disc and the rectangular plate is given to be m .
The radius of the disc is R while the length and breadth of the plate are l=2R and b=R respectively.
As seen in the figure, the distance between the two parallel axes AB and XX’ will be a=R+2R=23R .
The moment of inertia of the disc about its diameter is known to be Id=4mR2 .
Step 2: Express the moment of inertia of the rectangular plate based on the parallel axis theorem.
Consider an element of mass dm, breadth dx and length 2R at a distance x from the axis AB. This is shown in the figure below.
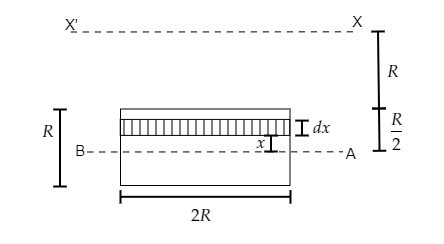
Then we can express the mass of the small element as dm=AmdA -------- (1) where A, dA are the areas of the plate and the element respectively.
The area of the plate will be A=l×b=2R×R=2R2 and the area of the element will bedA=l×dx=2Rdx .
Substituting for A=2R2 and dA=2Rx in equation (1) we get, dm=2R2m2Rdx=Rmdx .
Here the radius of gyration is k=x .
Then the moment of inertia of the element will be dI=dm×x2
Now the moment of inertia of the plate will be IAB=20∫R/2dI=20∫R/2Rmdx×x2
On integrating and applying the limits we have, IAB=R2m[3x3]0R/2=R2m(8×3R3)
⇒IAB=12mR2
Thus the moment of inertia of the rectangular plate about its length is IAB=12mR2.
Now the moment of inertia of the rectangular plate about the axis XX’ as given by the parallel axis theorem will be Irp=IAB+m(23R)2 ; 23R is the distance between AB and XX’.
Substituting for IAB=12mR2 in the above expression we get, Irp=12mR2+m(23R)2
⇒Irp=12mR2+49mR2=1228mR2
And finally, we have the moment of inertia of the plate about XX’ as Irp=37mR2
Step 3: Express the moment of inertia of the system.
The moment of inertia of the system about XX’ is the sum of the moment of inertia of disc and that of the rectangular plate about the axis XX’.
i.e., Isystem=Id+Irp -------- (2)
Substituting for Id=4mR2 and Irp=37mR2 in equation (2) we get, Isystem=4mR2+37mR2
⇒Isystem=123mR2+28mR2=1231mR2
Thus the moment of inertia of the system about XX’ is Isystem=1231mR2 .
Note: The integral of x2 is obtained as 3x3 by the general formula ∫xndx=n+1xn+1. The axis XX’ is mentioned to be passing through the centre of the disc. So the moment of inertia of the disc about its diameter will be equal to the moment of inertia of the disc about the axis XX’.
