Question
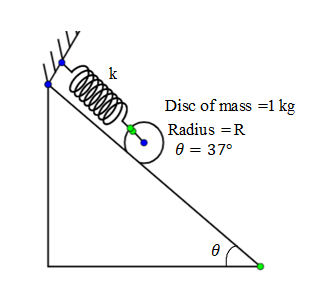
Question: A disc of mass m is connected to an ideal spring of force constant ‘k’. If the disc is released from...
A disc of mass m is connected to an ideal spring of force constant ‘k’. If the disc is released from rest then what is the maximum friction force on the disc (in N). Assuming friction is sufficient for pure rolling.
Solution
Friction is defined as the resistive force which opposes the motion of anybody if the surface of contact is not smooth. The acceleration on the disc will be different and be normal acceleration due to gravity as the disc is on the inclined plane.
Formula used:
The formula of the friction is given by,
⇒f=μ×N
Where the friction is μ and the normal reaction is N.
The formula of the normal reaction at inclined plane is given by,
⇒N=mgcosθ
Where mass is m the acceleration due to gravity is g and angle is inclination isθ.
Complete step by step answer:
It is given in the problem that a disc of mass m is connected to an ideal spring of force constant ‘k’ if the disc is released from rest then we need to find the maximum friction force on the disc in Newton.
The normal reaction of the disc is given by,
⇒N=mgcosθ………eq. (1)
Where mass is m the acceleration due to gravity is g and angle is inclination isθ.
The formula of the friction is given by,
⇒f=μ×N………eq. (2)
Where the friction isμ and the normal reaction is N.
Replacing the value of normal reaction in the equation (2) we get,
⇒f=μ×N
⇒f=μ×mgcosθ
The maximum friction is equal to,
⇒fmax.=μ×mgcosθ
Mass is 1 kg, and θ=37∘ therefore we get,
⇒fmax.=μ×mgcosθ
⇒fmax.=μ×9⋅8×cos37∘
⇒fmax.=μ×9⋅8×0⋅79864
⇒fmax.=7⋅827μ(N).
The maximum friction on the disc is equal tofmax.=7⋅827μ(N).
Note:
The students are advised to understand and remember the formula of the friction and the normal reaction on the inclined plane .The spring will try to stop the disc and after some extension of the spring the disc will stop also the friction will also oppose the motion of the disc.
