Question

A disc of mass M and radius R is rolling purely with centre’s velocity ${v}_\mathbf{0}$ on a flat horizontal floor when it hits a step in the floor of height $\dfrac{R}{\mathbf{4}}$. The corner of the step is sufficiently rough to prevent any slipping of the disc against itself. What is the velocity of the centre of the disc just after impact?
A) $\dfrac{\mathbf{4}{v}_\mathbf{0}}{\mathbf{5}}$
B) $\dfrac{\mathbf{4}{v}_\mathbf{0}}{\mathbf{7}}$
C) $\dfrac{\mathbf{5}{v}_\mathbf{0}}{\mathbf{6}}$
D) none of these

Answer 1

This question can be solved by the concept of conservation of momentum. The amount of momentum remains constant; momentum is neither created nor destroyed, but only changed through the action of forces described by Newton’s laws of motion.

Complete step by step answer:
Let us understand this question by pictorial representation.

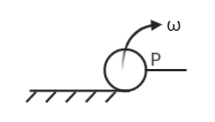
Angular momentum will remain conserved at the point of impact P and just after impact, it starts rotating about point P.
As per conservation of momentum, the total momentum is always constant for a system.
$L_i=L_f$
Where $L_i$ and $L_f$ are initial and final angular momentum.
$Mv_0(R-\dfrac{R}{4})+\dfrac{1}{2}MR^2(\dfrac{v_0}{R})=\dfrac{3}{2}MR^2\omega$ (M is common on both sides; hence we can cancel the term ‘M’)
Where M is the mass of disc, $v_0$ is the velocity at the centre of disc, R is the height from the floor and $\omega$ is the angular velocity.
$\implies v_0(R-\dfrac{R}{4})+\dfrac{1}{2}R^2(\dfrac{v_0}{R})=\dfrac{3}{2}R^2\omega$
Now, we further simplify the equation,
$v_0R-\dfrac{Rv_0}{4}+\dfrac{1}{2}R^2(\dfrac{v_0}{R})=\dfrac{3}{2}R^2\omega$ (Since R is common, we can cancel the term)
$v_0-\dfrac{v_0}{4}+\dfrac{1}{2}v_0=\dfrac{3}{2}R\omega$
Cross multiplying the equation,
${2v}_0-\dfrac{{2v}_0}{4}+\dfrac{2}{2}v_0=3R\omega$
$\implies {2v}_0-\dfrac{v_0}{2}+v_0=3R\omega$
Take LCM and simplify further, we get
$\dfrac{4v_0-v_0+2v_0}{2}=3R\omega$
$\implies \dfrac{5v_0}{2}=3R\omega$
$\implies 5v_0=6R\omega$
Now, we arrange the equation in terms of \omega to find velocity,
$\omega=\dfrac{5v_0}{6}$

Hence, the correct answer is “Option C”.

Note:
In an isolated system (such as the universe), there are no external forces, so momentum is always conserved. In mechanics, momentum, energy and angular momentum are the quantities conserved.