Question
Question: A disc of mass M and radius is rolling with angular speed on a horizontal plane as shown in the figu...
A disc of mass M and radius is rolling with angular speed on a horizontal plane as shown in the figure the magnitude of angular momentum of the disc about the origin O is:
(A) 21MR2ω
(B) MR2ω
(C) 23MR2ω
(D) 2MR2ω
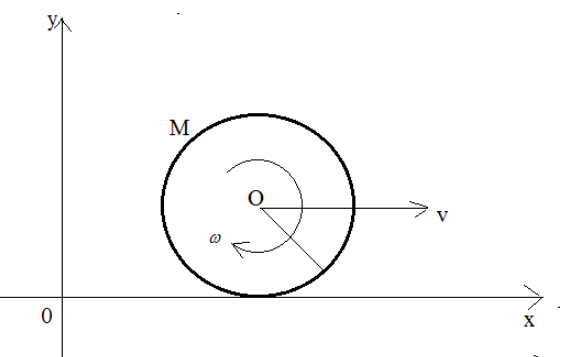
Solution
In this question, we need to determine the magnitude of angular momentum of the disc about the origin O such that a disc of the disc of mass M and radius is rolling with angular speed ω on a horizontal plane. For this, we will use the relation between the mass of the disc, radius of the disc and the angular speed of the disc.
Complete step by step answer:
Let the angular momentum about the origin be L0 which is given as the summation of the angular momentum with respect to the centre of mass of the disc and angular momentum with respect to the origin. Mathematically, L0=Iω+MvR where,
I = moment of inertia of the disc
ω = angular speed of the disc
v = speed of the disc on the plane and,
R = radius of the disc
There is no slipping involved in the motion, i.e. it’s a case of pure rolling, in that case, v = R
Also, the moment of inertia for the rolling disc is given by I=21MR2
Now, substituting values of v and I in the equation L0=Iω+MvR, we get
L0=21MR2ω+M(Rω)R ⇒L0=21MR2ω+M(R2ω) ∴L0=23MR2ω
Hence, the magnitude of angular momentum of the disc about the origin O is 23MR2ω.
Hence,option C is correct.
Note: It is worth noting here that the angular momentum of the translating rotating disc is the sum of the angular momentum due to the origin and due to the centre of mass of the disc.
