Question
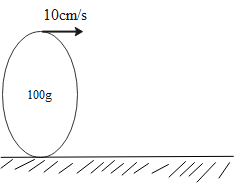
Question: A disc of mass \(100g\) is rolling without slipping on a horizontal surface with a velocity of \(10c...
A disc of mass 100g is rolling without slipping on a horizontal surface with a velocity of 10cm/s. Calculate its total energy.
Solution
When an object performs a rolling motion it means the object is performing two motions simultaneously. The rolling motion is constituted by the performance of rotational and translational motion by an object at the same time. The total energy of such a system is the total sum of the energy for both kinds of motion.
Formula to be used:
Etotal=RE+TE
Complete step by step answer:
As per the given data,
The mass (m) of the disc is 100g=0.1kg
The velocity (v0) of the body is 10cm/s=10×10−2m/s
When an object is rolling on a horizontal surface without slipping the energy is divided into performing two kinds of motion at a time. Rotational motion and other is the translational motion.
Energy for the rotational motion is known as the rotational kinetic energy. It is dependent on the moment of inertia of the object and the angular velocity by which it is rotating on its axis.
The rotational energy of a system is given by,
RE=21Iω2
Where,
I is the moment of inertia of the body
ω is the angular velocity of the object
This can be also written as,
RE=212mr2r2v2⇒RE=41mv2
The energy for the translational motion is known as the translational kinetic energy. It is dependent on the mass of the object and the velocity by which it is moving over a particular path. (Horizontal path for this case)
The translational kinetic energy is given as,
TE=21mv2
So here from the values of rotational and translational kinetic energy we can say that the total energy of the disc is,
Etotal=RE+TE⇒Etotal=41mv2+21mv2∴Etotal=43mv2
By putting the values as per the data given,
Etotal=43(0.1)(10×10−2)2Etotal=0.00075Etotal=7.5×10−4J
Thus, the total energy of the disc will be 7.5×10−4J. And this is the required answer.
Note:
The rotational kinetic energy is also known as the angular kinetic energy of the body. When an object performs a rolling motion only a small section of the surface of the body comes in contact with the surface on which it is moving. As a result, a very small amount of frictional force acts on the body and it is easy to displace the object easily.
