Question
Question: A disc of mass \(1\,kg\) of radius \(2\,m\) is moving with the velocity of \({\text{4 m}}{{\text{s}}...
A disc of mass 1kg of radius 2m is moving with the velocity of 4 ms−1 What is the kinetic energy of the disc?
A. 12 J
B. 8 J
C. 20 J
D. 10 J
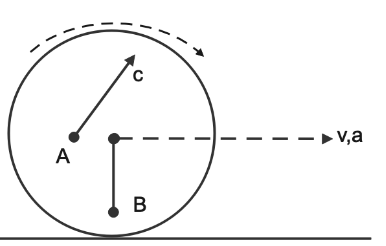
Solution
In order to solve the question, we will first find the translational kinetic energy and then we will find the rotational kinetic energy for which we have to find the moment of inertia of disc and angular velocity and then we after finding both the kinetic energy we will use them to find the total kinetic energy of disc
Formula used:
Formula of translational kinetic energy
KET=21mv2
Here, m refers to mass and v refers to velocity.
Formula of rotational kinetic energy
KER=21Iω2
Here, I refers to moment of inertia and ω refers to angular velocity.
Complete step by step answer:
In the question we are given a disc which is rotating as well as moving in the forward direction and we have to find the kinetic energy
Mass of the disc = 1 kg
Radius of the disc = 2 m
Velocity of the disc = 4 ms−1
On the disc two kinetic energies are applied transition kinetic energy and rotational kinetic energy hence
Total kinetic energy = Transition kinetic energy + Rotational kinetic energy
To find the Translational kinetic energy we will use the formula
KET=21mv2
We will substitute the value of mass and velocity in the equation
KET=21×1×42
⇒KET=21×1×42
Hence translation kinetic energy is
KET=8 J
To find the Rotational kinetic energy we will use the formula
KER=21Iω2
Now we have to find the moment of inertia of disc and the angular velocity of disc
Moment of inertia of disk = 2Mr2
Now we will substitute the value of radius and mass
I=21×(2)2
Hence the moment of inertia is
I = 2 Kg m2
Angular velocity of disk ω=rv
Now we will substitute the value of radius and velocity
ω=24=2s−1
Now we will substitute the value of momentum and angular velocity in the equation
KER=21Iω2
⇒KER=21×2×22
Hence Rotational kinetic energy is
KER=4 J
Total kinetic energy = Transition kinetic energy + Rotational kinetic energy
Transition kinetic energy = 8 J
Rotational kinetic energy = 4 J
Total kinetic energy = 8 J + 4 J
Thus total kinetic energy = 12 J
Hence, the correct option is A.
Note: Many of the students will make the mistake by not considering rotational kinetic energy as in the question we are given velocity, mass and radius but in diagram curve shows that disc is rotating so it produces both rotational and translational kinetic energy.
