Question

A disc is rolling on an inclined plane without slipping. Then what fraction of its total energy will be in the form of rotational kinetic energy?
A. $1\;:\;3$
B. $1\;:\;2$
C. $2\;:\;7$
D. $2\;:\;5$

Answer 1

First find the translational kinetic energy and rotational kinetic energy because If an object is in motion it can be divided into two parts: rotational motion and translational motion about the center of mass. After that, find total kinetic energy which is the sum of translational kinetic energy and rotational kinetic energy. The ratio is calculated by dividing rotational and total kinetic energy.

Formula used:
Translational kinetic energy, ${K_T} = \dfrac{1}{2}M{\nu ^2}$
Rotational kinetic energy, ${K_R} = \dfrac{1}{2}I{\omega ^2}$
Total kinetic energy, ${K_{total}} = {K_R} + {K_T}$
Moment of inertia of disc, $I{}_{disc} = \dfrac{2}{5}M{R^2}$

Complete step by step answer:

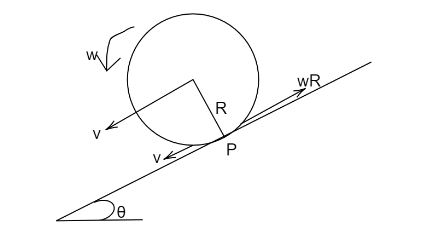
According to the question a disc is rolling on an inclined plane without slipping making an angle $\theta$ with the horizontal plane. Let The velocity be $\nu$ , rotating with angular velocity $\omega$ along the center of mass of the disc. At the point of contact $P$ the velocity ${\nu _P} = 0$.

If an object is in motion it can be divided into two parts: rotational motion and translational motion about the center of mass. velocity in upward direction will be $\omega R$ where $R$ is the radius of the sphere. Since ${\nu _P} = 0$ and both the velocities are in opposite directions, therefore, $\nu = \omega R$ where $\nu$ is the linear velocity of the sphere.

Now ${K_{total}} = {K_R} + {K_T}$
Translational kinetic energy,
$\Rightarrow {K_T} = \dfrac{1}{2}M{\nu ^2}$
where $M$is the mass of the disc
Since the disc is rotating about an axis passing through the center so rotational kinetic energy,
$\Rightarrow {K_R} = \dfrac{1}{2}I{\omega ^2}$
where $\omega$ is the angular velocity.
$\Rightarrow \dfrac{1}{2}\left( {\dfrac{2}{5}M{R^2}} \right){\omega ^2}$......$\because$ $I{}_{disc} = \dfrac{2}{5}M{R^2}$ , $\nu = \omega R$
$\Rightarrow \dfrac{{M{R^2}}}{5}{\left( {\dfrac{\nu }{R}} \right)^2}$
$\Rightarrow {K_R} = \dfrac{{M{\nu ^2}}}{5}$
$\Rightarrow {K_{total}} = \dfrac{{M{\nu ^2}}}{2} + \dfrac{{M{\nu ^2}}}{5}$
$\Rightarrow {K_{total}} = \dfrac{{7M{\nu ^2}}}{{10}}$
The fraction of its total energy associated with rotation
$\Rightarrow \dfrac{{{K_R}}}{{{K_{total}}}} = \dfrac{{\dfrac{{M{\nu ^2}}}{5}}}{{\dfrac{{7M{\nu ^2}}}{{10}}}}$
$\therefore \dfrac{{{K_R}}}{{{K_{total}}}} = \dfrac{2}{7}$

Therefore option C is the correct answer.

Note: When the body (circular disc) is rolling down the inclined plane, it has both rotational and translational kinetic energy i.e., rotational energy as the body is rotating while coming down the inclined plane and translational energy because it is coming straight from the inclined plane. For rolling without slipping conditions $\nu = r\omega$.