Question

A disc is placed on the surface of a pond which has a refractive index $\dfrac{5}{3}$ ​. A source of light is placed $4\,m$ below the surface of a liquid. Find the minimum radius of a disc so that light does not come out from a disc?

Answer 1

To solve this type of question firstly we will draw the diagram and then we will proceed with the solution. Here the depth is given from where the luminous object or source light is kept. And a disc is placed so that the light does not come out and we have to find that radius of the disc and to find that we will simply apply the $\sin$ formula to get the required solution.

Complete step by step answer:

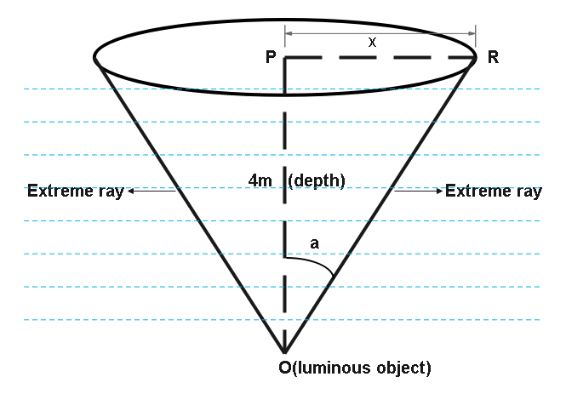
According to the question, the depth i.e., $OP = 4\,m$.
And refractive index i.e., $\mu = \dfrac{5}{3}$ .
Let us assume the radius of the disc is $PR = x$ .
And we know that,
$\sin a = \dfrac{1}{\mu } = \dfrac{3}{5}$
And from the figure we can say that,
$\sin a$ is nothing but perpendicular upon hypotenuse.
$\dfrac{{PR}}{{OR}} = \dfrac{3}{5}$
$\therefore PR = x = 3\,m$

Hence, the minimum radius of a disc so that light does not come out from a disc is $3\,m$.

Note: We can solve the above question in another way as solved below,
$x = \dfrac{{d(depth)}}{{\sqrt {{n^2} - 1} }} \\\ \Rightarrow x = \dfrac{4}{{\sqrt {{{\left( {\dfrac{5}{3}} \right)}^2} - 1} }} \\\$
On further solving,
$\Rightarrow x = \dfrac{4}{{\sqrt {\dfrac{{25}}{9} - 1} }} \\\ \Rightarrow x = \dfrac{4}{{\dfrac{4}{3}}} \\\ \therefore x = 3m \\\$
And remember that, the refractive index, often known as the index of refraction, is the measure of how much light changes direction in two media. In other words, the refractive index is a measurement of how much a light beam bends as it travels from one medium to another.