Question

A dipole is said to be in stable equilibrium when angle between electric field and dipole moment is
A). Zero
B). 180 degree
C). 45 degree
D). 90 degree

Answer 1

In this question, the dipole is kept in a uniform electric field. And we have to write the expressions for them in two different cases. So for solving this, we will keep the dipole at two positions and then, will find the dipole at $\theta = {0^ \circ }$ and at $\theta = {180^ \circ }$.
Formula used:
The potential energy of the dipole will be equal to the
$U = - P{E_0}\cos \theta$
And for torque, the formula will be
$\tau = P{E_0}\sin \theta$
Here,
$U$, will be the potential energy of the dipole
$\tau$, will be the torque
$P$, will be the electric dipole of the dipole moment
${E_0}$, will be the uniform electric field

Complete step-by-step solution:
Let us assume that the dipole we are using is kept at two positions namely (a) and (b) which is placed in a constant electric field ${E_0}$ as it is shown in the below diagram.

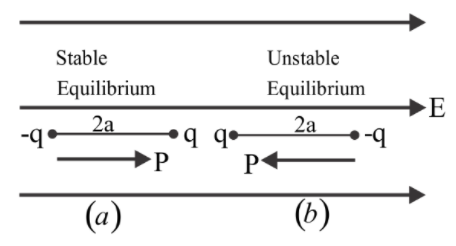
In the first case: When the angle between the dipole and electric field will be zero
Then, the Potential energy of the dipole will be equal to the
$U = - P{E_0}\cos \theta$
Therefore,
$U = - P{E_0}\cos {0^ \circ }$
And on simplifying the equation, we get
since $\cos {0^ \circ } = 1$
$U = - P{E_0}$
Therefore, we can say that the dipole will be in stable equilibrium.
Now we will find the torque,
And for torque, the formula will be
$\tau = P{E_0}\sin \theta$
$\Rightarrow \tau = P{E_0}\sin {0^ \circ }$
$\Rightarrow \tau = 0$
Hence, the option A is correct.
In the second case: When the angle between the dipole and electric field will be ${180}^{\circ}$
Then, the Potential energy of the dipole will be equal to the
$U = - P{E_0}\cos \theta$
$\Rightarrow U = - P{E_0}\cos {180^ \circ }$
$\Rightarrow U = P{E_0}$ $\left( {\therefore \cos {{180}^ \circ } = - 1} \right)$
Therefore, we can say that the dipole will be in unstable equilibrium.
Now we will find the torque,
And for torque, the formula will be
$\tau = P{E_0}\sin \theta$
$\Rightarrow \tau = P{E_0}\sin {180^ \circ }$
$\Rightarrow \tau = 0$

Note: Stable equilibrium means the lowest potential energy at the equilibrium point. Therefore the stable equilibrium the torque should be zero and the potential energy of the dipole should be minimum. Whereas the unstable equilibrium torque will be zero and the potential energy should be maximum or positive.