Question

A dip needle lies initially in the magnetic meridian when it shows an angle of dip $\theta$ at a place. The dip circle is rotated through an angle $x$ in the horizontal plane and then it shows an angle of dip $\theta^{\prime}$. Then $\dfrac{tan\theta^{\prime}}{tan\theta}$ is:
A. $\dfrac{1}{cos\;x}$
B. $\dfrac{1}{sin\;x}$
C. $\dfrac{1}{tan\;x}$
D. $cos\;x$

Answer 1

Recall that the dip angle is the angle that the earth’s magnetic field makes with the horizontal field with respect to the dip circle. When the dip circle is rotated, the horizontal component that aligns with the earth’s magnetic field will change and hence the dip angle will change as well. Use this to determine the expressions for the dip angles in both cases and a ratio comparison should yield the appropriate result.

Complete step-by-step answer:
We know that a dip needle or a dip circle is a compass that is pivoted to move in a plane containing the earth’s magnetic field. The angle that it measures, which is called the dip angle or the magnetic inclination is the angle that the earth’s magnetic field makes with the horizontal.
It makes use of the tendency of a magnet to align itself with the magnetic field lines.
Let us look at the dip needle in the context of our question. We initially have the dip needle in the plane of the magnetic meridian showing a dip angle of $\theta$.
From the figure, we see that the plane in consideration is the plane ABCD, and the dip angle, i.e., the angle between the horizontal $B_H$ and the earth’s magnetic field $B_V$ is:
$\Rightarrow tan\theta = \dfrac{B_V}{B_H}$

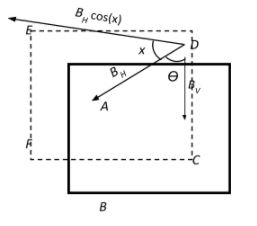
Now, the dip circle is rotated through an angle x in the horizontal plane, changing the dip angle to $\theta^{\prime}$.
Let this new plane be CDEF. Here, there is a component of the horizontal acting in this place, in addition to the earth’s magnetic field. Therefore,
$tan\theta^{\prime} = \dfrac{B_V}{B_H cos(x)}$
Dividing the two equations, we get:
$\dfrac{tan\theta^{\prime}}{tan\theta} =\dfrac{\left( \dfrac{B_V}{B_H cos(x)}\right)}{\left(\dfrac{B_V}{B_H}\right)}$
$\Rightarrow \dfrac{tan\theta^{\prime}}{tan\theta} = \dfrac{1}{cos(x)}$
Therefore, the correct choice would be A. $\dfrac{1}{cos\;x}$

So, the correct answer is “Option A”.

Note: Do not forget that the dip angle is in principle, the angle made by the needle of a vertically held compass, though in practice, ordinary compass needles may be weighted against dip to prevent any inconsistencies in directional information.
A dip needle has its application when travelling around the north and south poles. As we’ve seen, the dip needle measures the vertical magnetic inclination instead of the horizontal magnetic direction. When over the equator, the earth’s magnetic field is parallel to the surface of the earth, and as one approaches the poles, the magnetic field becomes more vertical since the field lines are directed into the surface of the earth. Thus, when directly over the magnetic poles, the dip needle points directly downward.